BÀI 4. VỊ TRÍ TƯƠNG ĐỐI VÀ GÓC GIỮA HAI ĐƯỜNG THẲNG. KHOẢNG CÁCH TỪ MỘT ĐIỂM ĐẾN MỘT ĐƯỜNG THẲNG

I. VỊ TRÍ TƯƠNG ĐỐI CỦA HAI ĐƯỜNG THẲNG

Bài 1: Xét vị trí tương đối của hai đường thẳng...

Giải rút gọn:

Ta có: . Do đó , cùng phương

Chọn điểm A(1; -2) . Thay toạ độ điểm A vào phương trình đường thẳng ta được: .

Vậy 2 đường thẳng và trùng nhau.

Bài 2: Xét vị trí tương đối của hai đường thẳng d...

Giải rút gọn:

+ Toạ độ giao điểm của đường thẳng d và là nghiệm của hệ phương trình:

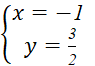=> Hệ có nghiệm duy nhất (−1; )

Vậy d ∩ ∆₁  tại điểm có tọa độ (−1; )

+ Toạ độ giao điểm của đường thẳng d và là nghiệm của hệ phương trình:

=> Hệ phương trình vô nghiệm.

Vậy d // .

+ Toạ độ giao điểm của đường thẳng d và là nghiệm của hệ phương trình:

=> Hệ phương trình vô số nghiệm.

Vậy d ≡ . 

II. GÓC GIỮA HAI ĐƯỜNG THẲNG

Bài 1: Tính số đo góc giữa hai đường thẳng...

Giải rút gọn:

a. Đường thẳng lần lượt có = (3; 3); .

cos( =  => (

b. Đường thẳng lần lượt có = (2; -1); .

cos( = => (

III. KHOẢNG CÁCH TỪ MỘT ĐIỂM ĐẾN MỘT ĐƯỜNG THẲNG

Bài 1: 

a. Tính khoảng cách từ điểm...

Giải rút gọn:

a.

d(O; ) =

b. Lấy M(0; 1)

BÀI TẬP CUỐI SGK 

Bài 1: Xét vị trí tương đối của mỗi cặp đường thẳng sau...

Giải rút gọn:

a. Toạ độ giao điểm của hai đường thẳng d₁, d₂ là nghiệm của hệ phương trình:

=> Hệ có 1 nghiệm duy nhất

Vậy 2 đường thẳng cắt nhau.

b. Toạ độ giao điểm của hai đường thẳng d₃, d₄ là nghiệm của hệ phương trình:

=> Hệ phương trình vô nghiệm 

Vậy 2 đường thẳng song song với nhau. 

c. Toạ độ giao điểm của hai đường thẳng d₅, d₆ tương ứng với t thoả mãn phương trình:

4

Phương trình này có nghiệm với mọi t nên 2 đường thẳng trùng nhau. 

Bài 2: Tính số đo góc giữa hai đường thẳng...

Giải rút gọn:

Đường thẳng d₁, d₂  có vectơ pháp tuyến là ;

=> cos (d₁, d₂)

Vậy (d₁, d₂) = 45^o

Bài 3: Tính khoảng cách từ một điểm đến...

Giải rút gọn:

a. d(A, ) =

b. Phương trình tổng quát của đường thẳng là: 2x + y + 3 = 0

=> d(B, ) =

Bài 4: Với giá trị nào của tham số m thì hai đường thẳng sau đây vuông góc...

Giải rút gọn:

Đường thẳng , có vectơ pháp tuyến là ;

Ta có:

Vậy m = - thì  

Bài 5: Cho ba điểm A...

Giải rút gọn:

Ta có:

cos

cos (AB, AC) =

Bài 6: Cho ba điểm A...

Giải rút gọn:

Gọi d là đường thẳng đi qua B và có vectơ pháp tuyến là

Vậy d: a(x + 1) + b(y – 2) = 0 ax + by + (a – 2b) = 0

Ta có: d(A, d) = d(C, d)

TH1: Chọn b = 1, a = 5, ta có phương trình đường thẳng d là: 5x + y + 5 -2 = 0 hay 5x + y + 3  = 0.

TH2: Chọn a = 1, b = 7, ta có phương trình đường thẳng d là: x + 7y + 1 – 2.7 = 0 hay x + 7y – 13 = 0. 

Vậy phương trình đường thẳng cần lập là 5x + y + 3 = 0 hoặc x + 7y – 13 = 0. 

Bài 7: Có hai  con tài A và B cùng xuất phát từ hai bến...

Giải rút gọn:

a. Tàu A di chuyển theo hướng vectơ

Tàu B di chuyển theo hướng vectơ

Gọi là góc giữa hai đường đi của hai tàu, ta có:

cos =

b. Sau t giờ:

+) Vị trí của tàu A là điểm M có tọa độ là: M(3 – 35t ; - 4 + 25t)

+) Vị trí của tàu B là điểm N có toạ độ là: N(4 – 30t ; 3 – 40t)

MN nhỏ nhất xấp xỉ 1,53 km khi t =

Vậy sau giờ kể từ thời điểm xuất phát thì hai tàu gần nhau nhất và cách nhau 1,53 km.