BÀI 5. PHƯƠNG TRÌNH ĐƯỜNG TRÒN

I. PHƯƠNG TRÌNH ĐƯỜNG TRÒN

Bài 1: Viết phương trình đường tròn tâm I(6;-4) đi qua điểm A(8;-7).

Giải rút gọn:

Bán kính đường tròn tâm I là: IA

Phương trình đường tròn là: 

Bài 2: Tìm k sao cho phương trình...

Giải rút gọn:

Để phương trình đã cho là phương trình đường tròn

hoặc .

Bài 3: Lập phương trình đường tròn đi qua ba điểm A(1;2); B(5;2); C(1;-3)

Giải rút gọn:

Giả sử I(a; b). Ta có: IA = IB = IC

Vì nên:

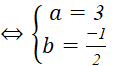=> I

Vậy R = IA =

Vậy phương trình đường tròn đi qua 3 điểm A, B, C là:

II. PHƯƠNG TRÌNH TIẾP TUYẾN CỦA ĐƯỜNG TRÒN.

Bài 1: Lập phương trình tiếp tuyến tại điểm M_o(-1;-4) thuộc đường tròn...

Giải rút gọn:

Đường tròn tâm I(3; -7)

Phương trình tiếp tuyến tại điểm M(-1; -4) thuộc đường tròn là:

(-1 – 3)(x + 1) + (-4 + 7)(y + 4) = 0 -4x + 3y + 8 = 0.

BAI TẬP CUỐI SGK

Bài 1: Phương trình nào sau đây là phương trình đường tròn...

Giải rút gọn:

a. x² + y² – 2x + 2y – 7 = 0 

Vậy đây là phương trình đường tròn có tâm I(1; -1), bán kính R = 3. 

b. x² + y² – 8x + 2y + 20 = 0 

(vô lí). 

Vậy đây không là phương trình đường tròn.

Bài 2: Tìm tâm và bán kính của đường tròn trong mỗi trường hợp sau...

Giải rút gọn:

a.

=> I(-1; 5) và R = 3. 

b. x² + y² – 6x – 2y -15 = 0

=> I(3; 1) và R = = 5. 

Bài 3: Lập phương trình đường tròn trong mỗi trường hợp sau...

Giải rút gọn:

a. Tâm O(-3; 4) và R = 9: 

=>

b. Tâm I (5; -2) và đi qua điểm M(4; -1) có bán kính MI

=>

c. Tâm I(1; -1) và tiếp tuyến

R = d(I; ) =

d. Đường kính AB với A(3; -4) và B(-1; 6) đi qua tâm I là trung điểm của AB.

I(1; 1) và R =

Có:

e. Đường tròn đi qua ba điểm A(1; 1); B(3; 1); C(0; 4)

Giả sử tâm đường tròn là I(a; b). 

Ta có: IA = IB = IC nên:

=> I(2; 3)

R = IC =

=>

Bài 4: Lập phương trình tiếp tuyến tại điểm có hoành độ bằng 3...

Giải rút gọn:

Đường tròn có tâm I(-2; -7) và R = 13.

Thay x = 3 vào phương trình đường tròn:

Do đó ta tìm được các: A(3; 5) và B(3; -19). 

Phương trình tiếp tuyến của đường tròn tâm I(-2; -7) tại điểm A(3; 5) là:

(3 + 2)(x – 3) + (5 + 7)(y – 5) = 0 

5x – 15 + 12y – 60 = 0 5x + 12y – 75 = 0.

Phương trình tiếp tuyến của đường tròn tâm I(-2; -7) tại điểm B(3; -19) là: 

 (3 + 2)(x – 3) + (-19 + 7)(y – (-19)) = 0 

5x – 15 - 12y – 243 = 0 5x - 12y – 243 = 0.

Bài 5: Tìm m sao cho đường thẳng 3x+4y+m=0 tiếp xúc với đường tròn...

Giải rút gọn:

: 3x + 4y + m = 0; (C):

Cótâm I(-1; 2), R = 2. 

d(I; ) = R

m + 5 = 10 hoặc m + 5 = -10 m = 5 hoặc m = -15. 

Bài 6: Hình 46 mô phỏng một trạm thu phát sóng điện thoại di động...

Giải rút gọn:

a. Tâm I(-2 ; 1) và R = 3.

=>

b. Ta có: M(-1 ; 3) 

=> IM =  

Ở vị trí có tọa độ (-1 ; 3) không thể sử dụng dịch vụ của trạm này. 

c. 

Giả sử vị trí đứng của người đó là B(-3 ; 4)

Vectơ pháp tuyến của (BI) là :

Phương trình tổng quát của (BI) : 3(x +2) + 1(y – 1) = 0 hay (BI) : 3x + y + 5 = 0. 

Gọi A = I ∩ (BI) Khoảng cách ngắn nhất để người đó di chuyển được từ vị trí B(-3 ; 4) tới vùng phủ sóng là AB. 

Toạ độ của A là nghiệm của hệ:

hoặc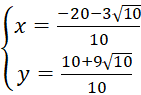

+ Với A => AB =

+ Với A => AB =

Do 0,2 < 6,2 nên ta chọn kết quả 0,2.

Bài 7: Ném đĩa là một môn thể thao thi đấu trong...

Giải rút gọn:

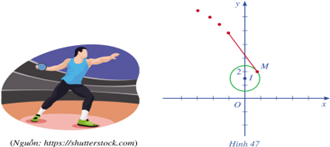
Quỹ đạo chuyển động của chiếc đĩa nằm trên tiếp tuyến của đường tròn tâm I tại điểm M. 

Vậy ta có phương trình là: