BÀI 2. GIẢI TAM GIÁC. TÍNH DIỆN TÍCH TAM GIÁC

I. GIẢI TAM GIÁC

II. TÍNH DIỆN TÍCH TAM GIÁC

Bài 1: Cho tam giác ABC có...

Giải rút gọn:

Ta có:

Áp dụng định lí sin trong tam giác ABC: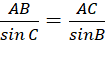

Diện tích △ABC là:  .

III. ÁP DỤNG VÀO BÀI TOÁN THỰC TIỄN

Bài 1: Từ trên nóc của một toà nhà cao...

Giải rút gọn:

Gọi A là vị trí đặt mắt quan sát bằng giác kế, B là vị trí ngọn cây, D là vị trí gốc cây, C là hình chiếu vuông góc của A lên BD.

+ Trường hợp 1: Cây cao hơn vị trí quan sát.

Gọi ,

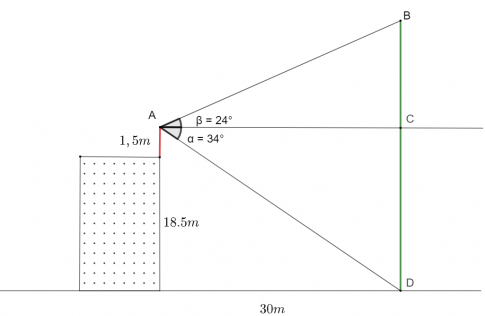
Áp dụng định lí sin trong △ABC: 

Mà

(m)

Vậy chiều cao của cây là: (m)

+ Trường hợp 2: Cây thấp hơn vị trí quan sát. 

Gọi ,

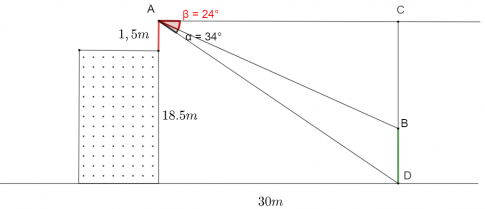
Áp dụng định lí sin cho △ABC:

(m)

Vậy chiều cao của cây là: (m)

BÀI TẬP CUỐI SGK

Bài 1: Cho tam giác ABC có BC...

Giải rút gọn:

a. Áp dụng định lí côsin:

.

b. Áp dụng định lí sin:

c. Diện tích △ABC là: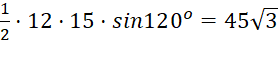 

Bài  2: Cho tam giác ABC...

Giải rút gọn:

Xét △ABC, ta có:

Áp dụng định lí sin: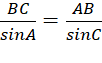  

Áp dụng định lí côsin:

. 

Bài 3: Cho tam giác ABC có AB...

Giải rút gọn:

a. Ta có:

Áp dụng định lí sin:

+

+

b. Diện tích △ABC là: 

Bài 4: Cho tam giác ABC có...

Giải rút gọn:

a. Áp dụng định lí côsin:

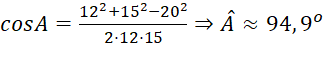
b. Diện tích △ABC là:  .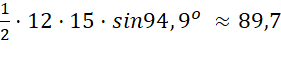 

Bài 5: Tính độ dài cạnh AB trong mỗi trường hợp sau...

Giải rút gọn:

Áp dụng định lí sin:

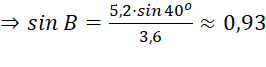
 hoặc

+ Trường hợp 1:

Áp dụng định lí sin: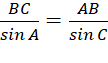

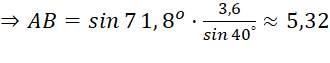
+ Trường hợp 2:

Áp dụng định lí sin: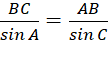

Vậy:  hoặc

Bài 6: Để tính khoảng cách giữa hai địa điểm A và B mà ta không...

Giải rút gọn:

AC = 1km = 1000 m.

Áp dụng định lí cosin:

Bài 7: Một người đi dọc bờ biển từ vị trí A đến vị trí B và quan sát...

Giải rút gọn:

Gọi C là vị trí ngọn hải đăng và H là hình chiếu vuông góc của C trên AB.

Khi đó CH là khoảng cách từ ngọn hải đăng tới bờ biển.

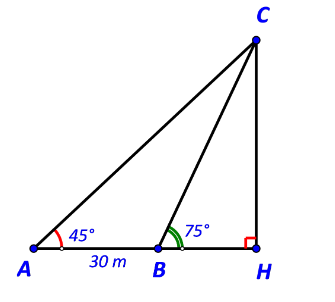
Ta có:,

Áp dụng định lí sin trong △ABC:

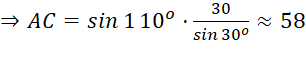
Xét △ACH có:

Vậy ngọn hải đăng cách bờ biển 41 m.