LT-VD 1: Cho tam giác $ABC$ có $ AB=12$; $\widehat{B}=60^{\circ}$; $\widehat{C}=45^{\circ}$. Tính diện tích của tam giác $ABC$.

Hướng dẫn giải:

Ta có: $\widehat{A}=180^{\circ}-\widehat{B}-\widehat{C}=75^{\circ}$

Áp dụng định lí sin: $\frac{AB}{sinC}=\frac{AC}{sinB}$ $\Rightarrow AC=\frac{AB \cdot sin B}{sinC} =6\sqrt{6}$

Diện tích tam giác $ABC$ là: $S=\frac{1}{2} \cdot AB \cdot AC \cdot sinA \approx 85,2$

LT-VD 2: Từ trên nóc của một toà nhà cao $18,5$m, bạn Nam quan sát một cái cây cách toà nhà $30$m và dùng giác kế đo được góc lệch giữa phương quan sát gốc cây và phương nằm ngang là $34^{\circ}$, góc lệch giữa phương quan sát ngọn cây và phương nằm ngang là $24^{\circ}$. Biết chiều cao của chân giác kế là $1,5$ m. Chiều cao của cái cây là bao nhiêu mét (làm tròn kết quả đến hàng phần mười)?

Hướng dẫn giải:

• Trường hợp 1: Cây cao hơn tòa nhà

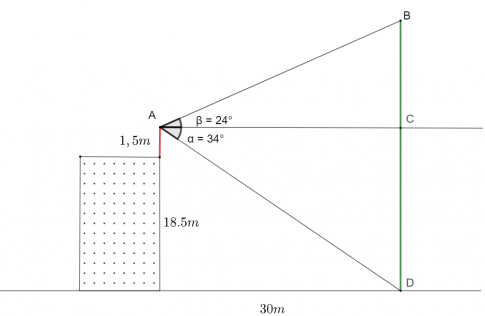
Áp dụng định lí sin: $\frac{BC}{sin\beta}=\frac{AC}{sin(90^{\circ}-\beta)}$

$\Rightarrow \frac{BC}{sin24^{\circ}}=\frac{30}{sin66^{\circ}}$

$\Rightarrow BC \approx 13,4$ (m)

Vậy chiều cao của cây là: $BD=BC+CD=18,5+13,4=31,9$ (m)

• Trường hợp 2: Tòa nhà cao hơn cây

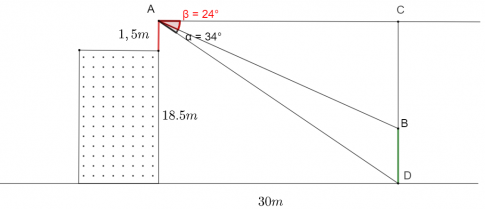
Áp dụng định lí sin: $\frac{BC}{sin\beta}=\frac{AC}{sin(90^{\circ}-\beta)}$

$\Rightarrow \frac{BC}{sin24^{\circ}}=\frac{30}{sin66^{\circ}}$

$\Rightarrow BC \approx 13,4$ (m)

Vậy chiều cao của cây là: $BD=DC-BC=18,5-13,4=5,1$ (m)