Giải câu 6 bài giải tam giác tính diện tích tam giác
Bài tập 6. Để tính khoảng cách giữa hai địa điểm $A$ và $B$ mà ta không thể đi trực tiếp từ $A$ đến $B$ (hai địa điểm nằm ở hai bên bờ một hồ nước, một đầm lầy...), người ta tiến hành như sau: Chọn một địa điểm $C$ sao cho ta đo được các khoảng cách $AC, CB$ và góc $ACB$. Sau khi đo, ta nhận được: $AC=1 \mathrm{~km}, CB=800 \mathrm{~m}$ và $\widehat{ACB}=105^{\circ}$ (Hình 31). Tính khoảng cách $AB$ (làm tròn kết quả đến hàng phần mười theo đơn vị mét).
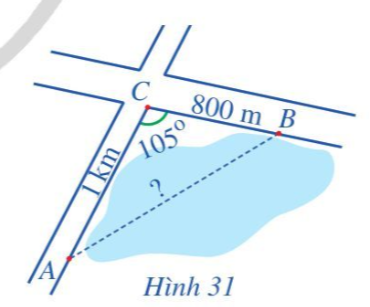
$A C$ = $1$ km = $1000$ m.
Áp dụng định lí cosin: $A B^{2}=A C^{2}+B C^{2}-2 \cdot A C \cdot B C \cdot \cos C $
$\Rightarrow A B^{2}=1000^{2}+800^{2}-2 \cdot 1000 \cdot 800 \cdot \cos 105^{\circ} $
$\Rightarrow A B = \sqrt{1000^{2}+800^{2}-2 \cdot 1000 \cdot 800 \cdot \cos 105^{\circ}} $
$\Rightarrow A B \approx 1433,2$
Vậy khoảng cách $AB$ là $1433,2$ m.
Xem toàn bộ: Giải bài 2 Giải tam giác. Tính diện tích tam giác

Bình luận