Giải bài 1 Giá trị lượng giác của một góc từ 0 đến 180. Định lí côsin và định lí sin trong tam giác
Giải bài 1 Giá trị lượng giác của một góc từ 0 đến 180. Định lí côsin và định lí sin trong tam giác - sách cánh diều toán 10 tập 1. Phần đáp án chuẩn, hướng dẫn giải chi tiết cho từng bài tập có trong chương trình học của sách giáo khoa. Hi vọng, các em học sinh hiểu và nắm vững kiến thức bài học.
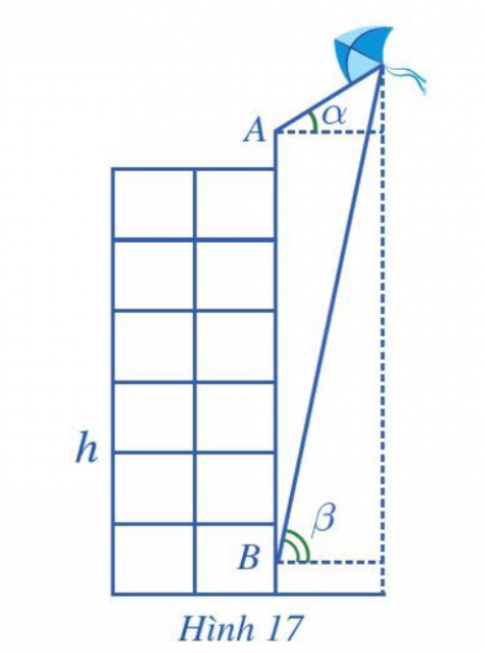
LT-VD 1: Hãy tính chiều cao $h$ của đỉnh Lũng Cú so với chân núi trong bài toán ở phần mở đầu.
Hướng dẫn giải:
Ta có $\left\{\begin{array}{l}tan\widehat{ACH}=\frac{AH}{CH} \\tan\widehat{BCH}=\frac{BH}{CH}\end{array}\right.$
$\Leftrightarrow \left\{\begin{array}{l}tan 45^{\circ}=\frac{h}{CH} \\tan 50^{\circ}=\frac{h+20,25}{CH}\end{array}\right.$
$\Rightarrow tan 50^{\circ}=\frac{h+20,25}{h} $
$\Rightarrow h \approx 106,6$ (m)
LT-VD 2: Cho tam giác ABC có $AB = 5$, $AC = 6$, $BC =7$. Tính $cosA$.
Hướng dẫn giải:
$cosA=\frac{AC^2+AB^2-BC^2}{2.AC.AB}=\frac{6^2+5^2-7^2}{2.6.5}=\frac{1}{5}$
LT-VD 3: Cho tam giác $ABC$ nội tiếp đường tròn $(O)$ có bán kính $R=6$ và có các góc $\widehat{B}=65^{\circ}, \widehat{C}=85^{\circ}$. Tính độ dài cạnh $BC$.
Hướng dẫn giải:
Ta có $\widehat{A}=180^{\circ}-\widehat{B}-\widehat{C}=180^{\circ}-65^{\circ}-85^{\circ}=30^{\circ}$
$BC = 2R.sin\widehat{A}=2R.sin30^{\circ}=6$
![90544]](https://s3.tech12h.com/sites/default/files/styles/inbody400/public/63_-_b1c4.png?itok=64oMIDa7)
Nội dung quan tâm khác
Thêm kiến thức môn học
Giải bài tập những môn khác
Giải SGK 10 KNTT
Giải SGK 10 CTST
Giải SGK 10 Cánh diều
Giải SBT lớp 10 kết nối tri thức
Giải SBT lớp 10 chân trời sáng tạo
Giải SBT lớp 10 Cánh diều
Giải chuyên đề học tập 10 Kết nối tri thức
Giải chuyên đề học tập 10 Chân trời sáng tạo
Giải chuyên đề học tập 10 Cánh diều
Trắc nghiệm 10 Kết nối tri thức
Trắc nghiệm 10 Chân trời sáng tạo
Trắc nghiệm 10 Cánh diều
Bình luận