Bài tập 1. Tìm tập xác định của mỗi hàm số sau:

a. $y=\frac{1}{x^{2}-x}$;

b. $y=\sqrt{x^{2}-4 x+3}$;

c. $y=\frac{1}{\sqrt{x-1}}$.

Hướng dẫn giải:

a. Biểu thức $y=\frac{1}{x^{2}-x}$ có nghĩa khi $x^{2}-x \neq 0$ $\Leftrightarrow \left\{\begin{array}{l}x \neq 0 \\ x -1\neq 0\end{array}\right.$ $\Leftrightarrow$ $\left\{\begin{array}{l}x \neq 0 \\ x \neq 1\end{array}\right.$ 

Vậy tập xác định của hàm số đã cho là $D=\mathbb{R} \setminus \{0;1\}$

b. Biểu thức $y=\sqrt{x^{2}-4 x+3}$ có nghĩa khi $x^{2}-4 x+3 \geq 0$ $\Leftrightarrow (x-1)(x-3) \geq 0$ $\Leftrightarrow \left\{\begin{array}{l}x \leq 1 \\ x\geq 3\end{array}\right.$

Vậy tập xác định của hàm số đã cho là $D=(-\infty;1] \cup [3;+\infty)$

c. Biểu thức $y=\frac{1}{\sqrt{x-1}}$ có nghĩa khi $x-1 > 0$ $\Leftrightarrow x>1$ 

Vậy tập xác định của hàm số đã cho là $D=(1;+\infty)$

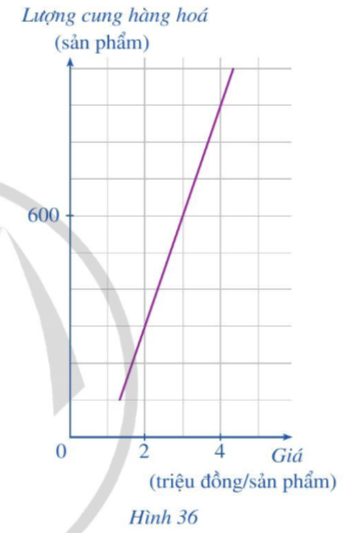
Bài tập 2. Đồ thị ờ Hình 36 cho thấy sự phụ thuộc của lượng hàng hoá được sản xuất (cung) (đơn vị: sản phẩm) vào giá bán (đơn vị: triệu đồng/sản phẩm) đối với một loại hàng hoá.

a. Xác định lượng hàng hoá được sản xuất khi mức giá bán 1 sản phẩm là 2 triệu đổng; 4 triệu đồng.

b. Biết nhu cầu thị trường đang cần là 600 sản phẩm. Hỏi với mức giá bán là bao nhiêu thì thị trường cân bằng (thị trường cân bằng khi sản lượng cung bằng sản lượng cầu)?

Hướng dẫn giải:

Từ đồ thị ta thấy:

a. Sản xuất được 300 sản phẩm khi mức giá bán 1 sản phẩm là 2 triệu đổng.

Sản xuất được 900 sản phẩm khi mức giá bán 1 sản phẩm là 4 triệu đổng.

b. Mức giá bán là 3 triệu đồng thì thị trường cân bằng.