BÀI TẬP CUỐI CHƯƠNG III 

Bài 1: Tìm tập xác định của mỗi hàm số sau...

Giải rút gọn:

a. y =

Biểu thức có nghĩa khi 0

Vậy D = \ {0;1}

b. y =

Biểu thức có nghĩa khi 0 (x – 1)(x – 3) 0

Vậy D = (-

c. y =

Biểu thức có nghĩa khi x – 1 > 0 x > 1

Vậy D = (1;+

Bài 2: Đồ thị ờ Hình 36 cho thấy sự phụ thuộc của...

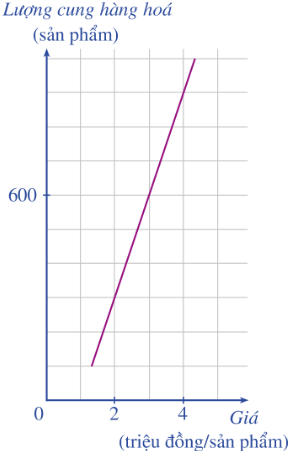
Giải rút gọn:

a. Sản xuất được 300 sản phẩm khi mức giá bán 1 sản phẩm là 2 triệu đồng.

Sản xuất được 900 sản phẩm khi mức giá bán 1 sản phẩm là 4 triệu đồng.

b. Mức giá bán là 3 triệu đồng thì thị trường cân bằng. 

Bài 3: Một nhà cung cấp dịch vụ Internet đưa ra hai gói...

Giải rút gọn:

a. Giả sử số thàng sử dụng Internet là x (nguyên dương, x 15).

Gọi y (đồng, y > 0) là số tiền phải trả khi dùng Internet. 

Gói A: y =

Gói B: y =

b. Số tiền gia đình bạn Minh dùng 15 tháng thì số tiền phải trả nếu:

• Dùng gói A: 190000.(15 – 2) = 2470000 (đồng)
• Dùng gói B: 2268000 đồng. 

Vậy gia đình bạn Minh nên dùng 15 tháng thì nên chọn gói B và trả tiền cước ngay 15 tháng.

Bài 4: Quan sát đồ thị hàm số bậc hai...

Giải rút gọn:

Bài 5: Vẽ đồ thị của mỗi hàm số sau...

Giải rút gọn:

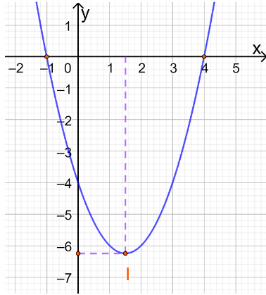
a. y = x² – 3x – 4

• Toạ độ đỉnh I
• Trục đối xứng x =
• Giao điểm của parabol với trục tung là (0;-4)
• Giao điểm của parabol với trục hoành là (-1;0) và (4;0)
• Điểm đối xứng với điểm (0;-4) qua trục đối xứng x = là (3;-4)

Ta nhận được đồ thị hàm số: 

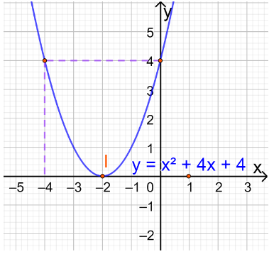
b. y = x² + 4x + 4

• Toạ độ đỉnh I
• Trục đối xứng x = -2
• Giao điểm parabol với trục tung là (0;4)
• Giao điểm parabol với trục hoành là (-2;0) 
• Điểm đối xứng với điểm (0;4) qua trục đối xứng x = 2 là (-4;4)

Ta nhận được đồ thị hàm số: 

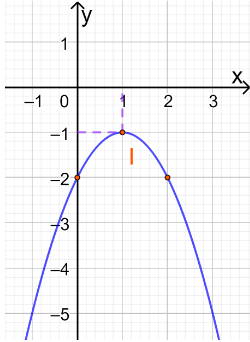
c. y = - x² + 2x – 2

• Toạ độ đỉnh I
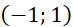
• Trục đối xứng x = 1
• Giao điểm parabol với trục tung là (0;-2)
• Giao điểm parabol với trục hoành là (0;-2) 
• Điểm đối xứng với điểm (0;-2) qua trục đối xứng x = 1 là (2;-2)

Ta nhận được đồ thị hàm số: 

Bài 6: Lập bảng xét dấu của mỗi tam thức bậc hai sau...

Giải rút gọn:

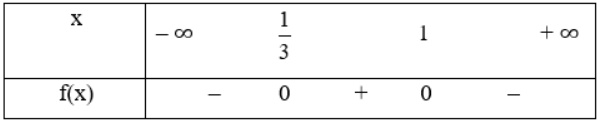
a. f(x) = -3x² + 4x -1

Tam thức bậc hai có a = -3 < 0, = 4² – 4 . (– 3) . (– 1) = 4 > 0 có 2 nghiệm phân biệt x₁ = ; x₂ = 1

Bảng xét dấu: 

b. f(x) = x² – x – 12

Tam thức bậc hai có a = 1 > 0, = (– 1)² – 4 . 1 . (– 12) = 49 > 0 có 2 nghiệm phân biệt x₁ = -3; x₂ = 4

Bảng xét dấu: 

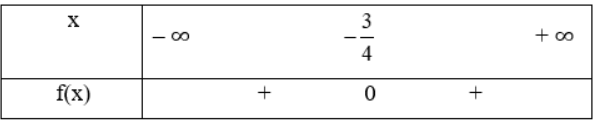
c. f(x) = 16x² + 24x + 9

Tam thức bậc hai có a = 16 > 0, = 24² – 4 . 16 . 9 = 0 có 2 nghiệm kép x =

Bảng xét dấu: 

Bài 7: Giải các bất phương trình sau...

Giải rút gọn:

a. Tam thức 2x² + 3x + 1 có 2 nghiệm phân biệt x = -1; x = hệ số a = 2 > 0

Bảng xét dấu: 

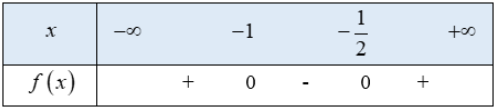
Vậy tập nghiệm của bất phương trình là (-

b. Tam thức -3x² + x + 1 có 2 nghiệm phân biệt x = ; x = hệ số a = -3 < 0

Bảng xét dấu: 

Vậy tập nghiệm của bất phương trình là (

c. Tam thức 4x² + 4x + 1 có nghiệm duy nhất x = hệ số a = 4 > 0

Bảng xét dấu: 

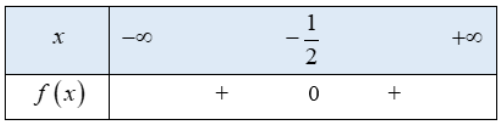
Vậy tập nghiệm của bất phương trình là .

d. Tam thức -16x² + 8x -1 có nghiệm duy nhất x = hệ số a = -16 < 0

Bảng xét dấu: 

Vậy tập nghiệm của bất phương trình là \

e. Tam thức 2x² + x + 3 có = -23 < 0 và có a = 2 > 0

Ta thấy tập hợp những giá trị của x sao cho tam thức 2x² + x + 3 mang dấu “-“ là

Vậy tập nghiệm của bất phương trình là

g. -3x² + 4x – 5 < 0. Tam thức -3x² + 4x – 5 có = -44 < 0 và có a = -3 < 0

Ta thấy tam thức 3x² + 4x – 5 < 0 với mọi x

Vậy tập nghiệm của bất phương trình là .

Bài 8: Giải các phương trình sau...

Giải rút gọn:

a. = x Ta có : x 0

x + 2 = x² x² – x – 2 = 0 

Vậy phương trình có nghiệm {2}

b. . 

2x² + 3x – 2 = x² + x + 6 

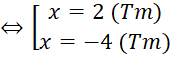
Vậy phương trình có nghiệm là {-4 ;2}

c. Ta có : x -3

2x² + 3x -1 = (x+3)² 

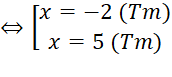
Vậy phương trình có nghiệm là {-2 ;5}

Bài 9: Một kĩ sư thiết kế đường dây điện từ vị trí A...

Giải rút gọn:

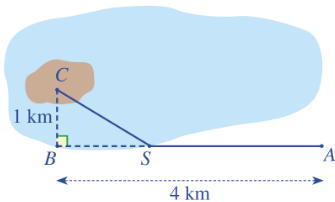
Gọi khoảng cách từ A đến S là x km (0 < x < 4). 

Ta có: 3.AS + 5.SC = 16 (triệu đồng) 

3.x + 5. 

25.(1 + (4 – x )²) = (16 – 3x)²  x = (thoả mãn)

Vậy tổng km đường dây điện đã thiết kế là:

AC = AS + SC = + = 4,5 (km).