BÀI TẬP CUỐI CHƯƠNG VI

Bài 1: Cho mẫu số liệu...

Giải rút gọn:

Mẫu số liệu theo thứ tự không giảm ta được: 1; 2; 4; 5; 9; 10; 11

a. Giải rút gọn C

b. Giải rút gọn A

Do mẫu số liệu trên có 7 số nên Q₂ = 5

c. Giải rút gọn D

Tứ phân vị của mẫu số liệu trên là: Q₁ = 2; Q₃ = 10

d. Giải rút gọn C

R = 11 – 1 = 10

e. Giải rút gọn B

g. Giải rút gọn B

s² =

h. Giải rút gọn A

s =

Bài 2: Bảng 6 thống kê số áo sơ mi nam...

Giải rút gọn:

Giải rút gọn D.

Ta thấy cỡ áo số 39 có tần số lớn nhất (47). Vậy mốt của mẫu số liệu là 39. 

Bài 3: Biểu đồ đoạn thẳng ở Hình 6...

Giải rút gọn:

a. Mẫu số liệu thống kê số lượt khách du lịch quốc tế đến Việt Nam là:

250  1 351  2 148    3 478       5 050       7 944         18 009

b. Mẫu số liệu theo thứ tự tăng dần là:

 250        1 351       2 148       3 478       5 050         7 944         18 009

Số trung bình cộng của mẫu số liệu trên là:

Trung vị Q₂ = 3 478

Trung vị của dãy 250; 1 351; 2 148 là: Q₁ = 1 351

Trung vị của dãy 5 050; 7 944; 18 009 là: Q₃ = 7 944

c. Khoảng biến thiên của mẫu số liệu là: R = 18 009 – 250 = 17 759

Khoảng tứ phân vị của mẫu số liệu trên là:

d. s² =

Bài 4: Lớp 10A có 40 học sinh...

Giải rút gọn:

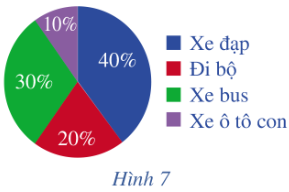
a. Só bạn đi xe đạp đến trường là: 40.40% = 16 (bạn)

b. n( =

Gọi A là biến cố “Bạn được chọn là bạn đến trường bằng xe đạp”

Số phần tử của biến cố A là: n(A) = = 16

Xác suất của biến cố A là: P(A) =

Bài 5: Em hãy tìm hiểu chiều cao...

Giải rút gọn:

Học sinh tự thực hiện dựa vào số liệu của lớp mình sau đó làm theo hướng dẫn sau:

a. Sắp xếp mẫu số liệu theo thứ tự không giảm: x₁, x₂, ... ,x_n

+ Số trung bình cộng:

+ Trung vị

Q₂ = M_e =

Q₁ là trung vị của nửa số liệu đã sắp xếp bên trái Q₂ (không bao gồm Q₂ nếu n lẻ)

Q₃ là trung vị của nửa số liệu đã sắp xếp bên phải Q₂ (không bao gồm Q₂ nếu n lẻ)

b. Khoảng biến thiên: R = x_n – x₁

Khoảng tứ phân vị:

c. Tính phương sai: s² =

Độ lệch chuẩn s =

Bài 6: Trong một hội thảo quốc tế...

Giải rút gọn:

Tổng số chuyên gia là: 10 + 12 = 22 (chuyên gia)

n() = (phần tử).

Gọi A là biến cố “Chọn được 2 chuyên gia ở hai châu lục khác nhau vào ban tổ chức”

TH1: Chọn 1 trong 10 chuyên gia ở châu Á, có 10 cách chọn.

TH2: Chọn 1 trong 12 chuyên gia ở châu Âu, có 12 cách chọn.

Số phần tử của biến cố A là: n(A) = 10.12 = 120 (phần tử)

Vậy xác suất của biến cố A là: P(A) =

Bài 7: Trong một buổi khiêu vũ có đúng 10 cặp vợ chồng...

Giải rút gọn:

10 cặp vợ chồng thì có tất cả 20 người.

n() = (phần tử)

Gọi A là biến cố “Chọn được 2 người là vợ chồng”

Vì có 10 cặp nên chọn được 2 người là vợ chồng thì có 10 cách chọn.

Số phần tử của biến cố A là: n(A) = (phần tử)

Vậy xác suất của biến cố A là: P(A) =

Bài 8: Một lô hàng có 20 sản phẩm bao gồm 16 chính...

Giải rút gọn:

a. Số kết quả xảy ra khi chọn ngẫu nhiên 3 sản phẩm là: (kết quả)

b. n() = 1 140 (phần tử).

Gọi A là biến cố “Cả 3 sản phẩm được chọn là chính phẩm”

Ta chọn 3 trong 16 chính phẩm nên số phần tử của biến cố A là: n(A) = (phần tử)

Vậy xác suất của biến cố A là: P(A) =

Bài 9: Trong một hộp có 20 chiếc thẻ...

Giải rút gọn:

n () = (phần tử) 

Gọi A là biến cố “Tích các số trên hai thẻ là số lẻ”.

Để tích các số trên thẻ là số lẻ thì cả hai thẻ bốc được đều phải là số lẻ vậy nên ta phải chọn ngẫu nhiên 2 thẻ từ 10 thẻ số lẻ. 

Nên số phần tử các kết quả thuận lợi cho A là: n(A) = (phần tử)

Vậy xác suất của biến cố A là: P(A) =