BÀI TẬP CUỐI CHƯƠNG II

Bài 1: Biểu diễn miền nghiệm của mỗi bất phương trình sau...

Giải rút gọn:

a) 3x - y > 3;

Vẽ đường thẳng d: 3x – y = 3. 

Lấy điểm O (0; 0). Ta có: 3. 0 – 0 = 0 < 3 (vô lí)

Vậy miền nghiệm của bất phương trình là nửa mặt phẳng không bị gạch.

b) x + 2y ≤ -4;

Vẽ đường thẳng d: x + 2y = −4. 

Lấy điểm O (0; 0). Ta có 0 + 2. 0 = 0 ≤ −4 (vô lí).

Vậy miền nghiệm của bất phương trình là nửa mặt phẳng không bị gạch.

c) y ≥ 2x - 5 2x - y ≤ 5

Vẽ đường thẳng d: 2x - y = 5.  

Lấy điểm O (0; 0). Ta có: 2. 0 - 0 = 0 ≤ 5 (luôn đúng)

Vậy miền nghiệm của bất phương trình là nửa mặt phẳng không bị gạch.

Bài 2: Biểu diễn miền nghiệm của mỗi hệ bất phương trình sau...

Giải rút gọn:

a)

• Trong cùng mặt phẳng tọa độ Oxy, vẽ đường thẳng: 

d₁: 2x − 3y = 6. 

d₂: 2x + y = 2.

• Gạch đi các phần không thuộc miền nghiệm của mỗi bất phương trình. Miền nghiệm của hệ bất phương trình là phần không bị gạch (chứa điểm O (0; 0), không kể các đường thẳng tương ứng).

b)

• Trong cùng mặt phẳng tọa độ Oxy, vẽ đường thẳng: 

d₁: 2x + 5y = 10; 

d₂: x − y = 4; 

d₃: x = −2.

• Gạch đi các phần không thuộc miền nghiệm của mỗi bất phương trình. Miền nghiệm của hệ bất phương trình là miền tam giác ABC kể cả biên.

c)

• Trong cùng mặt phẳng tọa độ Oxy, vẽ đường thẳng:

d₁: x − 2y = 5; 

d₂: x + y = 2; 

d₃: x = 0; 

d₄: y = 3

• Gạch đi các phần không thuộc miền nghiệm của mỗi bất phương trình. Miền nghiệm của hệ bất phương trình là miền tứ giác ABCD kể cả biên.

Bài 3: Nhu cầu canxi tối thiểu cho một người đang độ tuổi trưởng thành...

Giải rút gọn:

a) Lượng canxi có trong x lạng đậu nành là 165x (mg), y lạng thịt là 15y (mg)

Ta có bất phương trình: 165x + 15y ≥ 1 300

b) Thay x = 10, y = 5 ta có: 

165. 10 + 15. 5 = 1 725 > 1 300 (Luôn đúng) 

Vậy (10; 5) là một nghiệm của hệ bất phương trình.

Bài 4: Bác Ngọc thực hiện chế độ ăn kiêng qua thức uống với yêu...

Giải rút gọn:

a) Gọi số lượng cốc cho đồ uống thứ nhất và thứ hai cần tìm lần lượt là x, y (x, y ∈ )

Lượng calo trong cả 2 đồ uống là: 60x + 60y

Lượng vitamin A trong 2 đồ uống là: 12x + 6y

Lượng vitamin C trong 2 đồ uống là: 10x + 30y

Ta có hệ bất phương trình: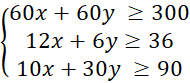

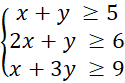
b) Thay x = 2, y = 3 ta có:

• 2 + 3 = 5 ≥ 5 (Luôn đúng)

• 2. 2 + 3 = 7 ≥ 6 (Luôn đúng)

• 2 + 3. 3 = 11 ≥ 9 (Luôn đúng)

⇒ (2; 3) là nghiệm của hệ bất phương trình.

Thay x = 5, y = 2 ta có: 

• 5 + 2 = 7 ≥ 5 (Luôn đúng)

• 2. 5 + 2 = 12 ≥ 6 (Luôn đúng)

• 5 + 3. 2 = 11 ≥ 9 (Luôn đúng)

⇒ (5; 2) là nghiệm của hệ bất phương trình.

Vậy bác Ngọc có thể chọn lựa 2 cốc cho đồ uống thứ nhất và 3 cốc cho đồ uống thứ hai hoặc 5 cốc cho đồ uống thứ nhất và 2 cốc cho đồ uống thứ hai.

Bài 5: Một chuỗi nhà hàng ăn nhanh bán đồ ăn từ...

Giải rút gọn:

Gọi số nhân viên ca I và ca II lần lượt là x, y (x, y *)

Lương làm việc 1 ngày của ca I là: 20 000. 8 = 160 000 (đồng)

Lương làm việc 1 ngày của ca 2 là: 22 000. 8 = 176 000 (đồng)

Tổng chi phí tiền lương mỗi ngày là: T = 160 000x + 176 000y (đồng)

Ta có hệ bất phương trình: 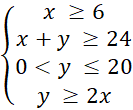 sao cho biểu thức T có giá trị nhỏ nhất.

Ta xác định miền nghiệm của hệ bất phương trình bằng cách vẽ đồ thị.

Miền nghiệm của hệ bất phương trình là miền tứ giác ABCD với A(6; 18), B(6; 20), C(10; 20), D(8; 16).

Biểu thức T = 160 000x + 176 000 y có giá trị nhỏ nhất tại một trong các đỉnh của tứ giác ABCD. Thay lần lượt các tọa độ của tứ giác, ta được:

T_A = 160 000. 6 + 176 000. 18 = 4 128 000

T_B = 160 000. 6 + 176 000. 20 = 4 480 000

T_C = 160 000. 10 + 176 000. 20 = 5 120 000

T_D = 160 000. 8 + 176 000. 16 = 4 096 000 (Chọn)

Vậy để chi phí tiền lương mỗi ngày là ít nhất thì chuỗi nhà hàng cần huy động 8 nhân viên ca I và 16 nhân viên ca II, khi đó chi phí tiền lương cho 1 ngày là 4096000 đồng.