BÀI TẬP CUỐI CHƯƠNG IV

Bài 1: Cho tam giác ABC có...

Giải rút gọn:

a. Áp dụng định lý cosin: BC =

Áp dụng định lý sin:  

b.

c. S_ABC =

d. Ta có: S =

(H là chân đường cao) 

e.

Do M là trung điểm của BC nên ta có:

Bài 2: Không dùng máy tính cầm tay...

Giải rút gọn:

A = (sin 20⁰ + sin 70⁰)² + (cos 20⁰ + cos 110⁰)²

= (cos 70⁰ + cos 20⁰)² + (cos 20⁰ + cos 110⁰)²

= (- cos 110⁰ + cos 20⁰)² + (cos 20⁰ + cos 110⁰)²

= 2((cos 20⁰)² + (cos 110⁰)²)

= 2((sin 70⁰)² + (-cos 70⁰)²) = 2

B = tan 20⁰ + cot 20⁰ + tan 110⁰ + cot 110⁰

= cot 70⁰ + tan 70⁰ – tan 70⁰ – cot 70⁰  = 0 

Bài 3: Không dùng thước đo góc, làm thế nào để biết số đo góc đó...

Giải rút gọn:

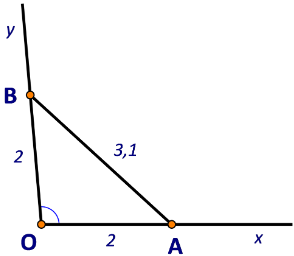
Áp dụng định lí cosin trong △OAB, ta có: 

cos O =

Bài 4: Có hai trạm quan sát A và B ven hồ và một...

Giải rút gọn:

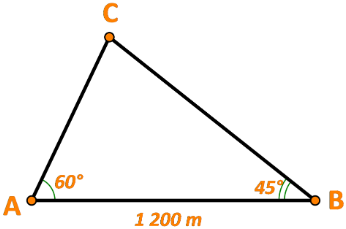
Ta có = 180⁰ - - = 75⁰

Áp dụng định lý sin:

1075,9 (m)

878,5 (m) 

Bài 5: Một người đứng ở bờ sông, muốn đo độ rộng của khúc sông...

Giải rút gọn:

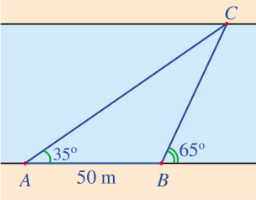
Ta có: = 65⁰ – 35⁰ = 30⁰ (tính chất góc ngoài tại đỉnh B của tam giác) 

Áp dụng định lí sin trong △ABC ta có: 

Độ rộng của khúc sông là: AC.sin A = 90,63.sin 35⁰ 52 (m).

Bài 6: Để đo khoảng cách giữa hai vị trí M,N ở hai phía ốc đảo...

Giải rút gọn:

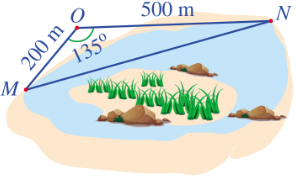
Áp dụng định lý côsin trong △OMN:

MN² =

=> MN = (m)

Bài 7: Chứng minh...

Giải rút gọn:

a. 

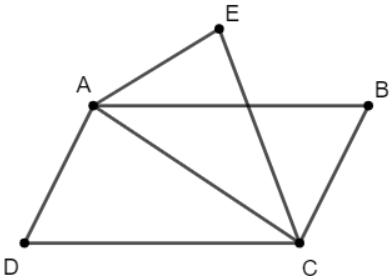
Vì ABCD là hình bình hành nên

Với điểm E bất kì ta có: (đpcm)

b. 

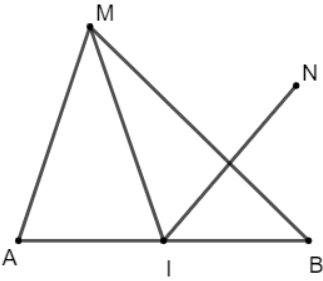
Vì I là trung điểm của AB nên với điểm M bất kì ta có:

Do đó với điểm N bất kì, ta có:  

c. 

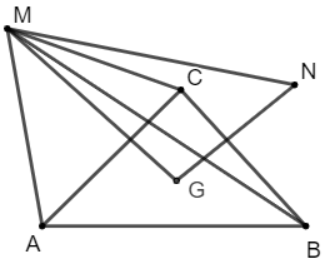
Do G là trọng tâm của △ABC nên 

Với điểm M bất kì ta có:  

Với điểm N bất kì ta có:

Bài 8: Cho hình bình hành ABCD có...

Giải rút gọn:

a. ;

b.

c. Áp dụng định lí cosin cho △ABD ta có:

BD² =

=> BD =

Áp dụng định lí cosin cho △ABC ta có: 

AC² =

=> AC =

Bài 9: Hai lực...

Giải rút gọn:

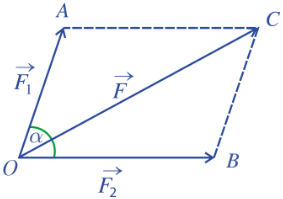
Áp dụng quy tắc hình bình hành:

Áp dụng định lý cosin: 

Vậy cường độ của hợp lực là: