Giải câu 5 bài giải tam giác tính diện tích tam giác

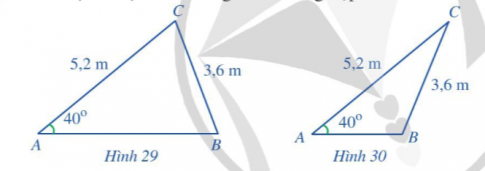
Áp dụng định lí sin:$\frac{B C}{\sin A}=\frac{A C}{\sin B}$

$\Rightarrow \sin B=\frac{A C \cdot \sin A}{B C}=\frac{5,2 \cdot \sin 40^{\circ}}{3,6} \approx 0,93 $

$\Rightarrow \widehat{B} \approx 68,2^{\circ} \text { hoặc } \widehat{B} \approx 111,8^{\circ}$

a. Với $\widehat{B} \approx 68,2^{\circ}$

$\widehat{C}=180^{\circ}-\widehat{A}-\widehat{B}=180^{\circ}-40^{\circ}-68,2^{\circ}=71,8^{\circ}$

Áp dụng định lí sin: $\frac{B C}{\sin A}=\frac{A B}{\sin C}$

$\Rightarrow A B=\sin C \cdot \frac{B C}{\sin A}=\sin 71,8^{\circ} \cdot \frac{3,6}{\sin 40^{\circ}} \approx 5,32$

b. Với $\widehat{B} \approx 111,8^{\circ}$

$\widehat{C}=180^{\circ}-\widehat{A}-\widehat{B}=180^{\circ}-40^{\circ}-111,8^{\circ}=28,2^{o}$

Áp dụng định lí sin: $\frac{B C}{\sin A}=\frac{A B}{\sin C}$

$\Rightarrow A B=\sin C \cdot \frac{B C}{\sin A}=\sin 28,2^{\circ} \cdot \frac{3,6}{\sin 40^{\circ}} \approx 2,65$

Vậy:

a. $AB=5,32$ 

b. $AB=2,65$