I. GIẢI TAM GIÁC 

Giải tam giác là tính các cạnh và các góc của tam giác dựa trên những dữ kiện cho trước.

HĐ1: 

Áp dụng định lí côsin trong tam giác ABC có:

$BC^2=AB^2+AC^2-2.AB.AC.\cos A =c^2+b^2=2.b.c.\cos a$

⇒ $BC= \sqrt{c^2+b^2-2bc \cos a}$

Ví dụ 1 (SGK -tr72)

HĐ2: 

Áp dụng định lí côsin trong tam giác ABC: $\cos A= \frac{b^2+c^2-a^2}{2bc}$

Ví dụ 2 (SGK -tr73)

HĐ3: 

$\widehat{A}=180^{\circ}-(\widehat{B}+\widehat{C})=180^{\circ}-(\alpha+\beta)$

$\sin A = \sin (\alpha+\beta)$

Áp dụng định lí sin trong tam giác ABC:

$\frac{BC}{\sin A}= \frac{AC}{\sin B} = \frac{AB}{\sin C}= 2R$

$\frac{a}{\sin (\alpha+\beta)}= \frac{AC}{\sin a}= \frac{AB}{\sin \beta}= 2R$

⇒ $AC= \frac{a.\sin a}{\sin (\alpha+\beta)}; AB= \frac{a. \sin \beta}{\sin (\alpha+\beta)}$

Ví dụ 3 (SGK -tr73)

II. TÍNH DIỆN TÍCH TAM GIÁC

HĐ4 (SGK -tr74)

Kết luận:

Cho tam giác ABC có $BC = a, CA = b, AB = c$. Khi đó, diện tích S của tam giác ABC là:

$S=\frac{1}{2}bc\sin A= \frac{1}{2}ca\sin B= \frac{1}{2}ab\sin C$

Ví dụ 4 (SGK -tr74)

Luyện tập 1:

Ta có: $\widehat{A}= 180^{\circ} - \widehat{B} - \widehat{C}= 75^{\circ}$

Áp dụng định lí sin trong tam giác ABC: 

$\frac{AB}{\sin C}= \frac{AC}{\sin B} \Rightarrow AC= \frac{AB.\sin B}{\sin C}= 6\sqrt{6}$

Diện tích tam giác ABC là: 

$S= \frac{1}{2}. AB. AC. \sin{A} ≈ 85,2$.

HĐ5:

Theo định lí côsin, ta có:

$\cos A= \frac{b^2+^c2-a^2}{2bc}$

Mà $A+A= 1$

$\Rightarrow A= \frac{4b^2c^2-(b^2+c^2-a^2)^2}{4b^2c^2}$

$\sin A= \frac{1}{2bc}\sqrt{(2bc)^2-(b^2+c^2-a^2)^2}$

Xét $T= (2bc)^2-(b^2+c^2-a^2)^2$

= $(2bc+b^2+c^2-a^2)(2bc-b^2-c^2+a^2)=[(b+c)^2-a^2][a^2-(b-c)^2]$

= $(b+c-a)(b+c+a)(a-b+c)(a+b-c)$

Ta có: $a + b = c = 2p$

$\Rightarrow b+c-a=2(p-a) a-b+c=2(p-b) a+b-c=2(p-c)$

⇒ $T=4\sqrt{p(p-a)(p-b)(p-c)}$

Vậy $\sin A= \frac{2}{bc}\sqrt{p(p-a)(p-b)(p-c)}$ 

b) Diện tích S theo các cạnh của tam giác ABC 

$S= \frac{1}{2}bc\sin A$

= $\frac{1}{2}bc.\frac{2}{bc}\sqrt{p(p-a)(p-b)(p-c)}= \sqrt{p(p-a)(p-b)(p-c)}$

Kết luận:

Cho tam giác ABC có $BC = a, CA = b, AB = c, p = \frac{a+b+c}{2}$. Khi đó, diện tích S của tam giác ABC là: $S=\sqrt{p(p-a)(p-b)(p-c)}$

Ví dụ 5 (SGK -tr75)

III. ÁP DỤNG VÀO BÀI TOÁN THỰC TIỄN

Ví dụ 6 (SGK -tr75)

Ví dụ 7 (SGK -tr75)

Luyện tập 2: 

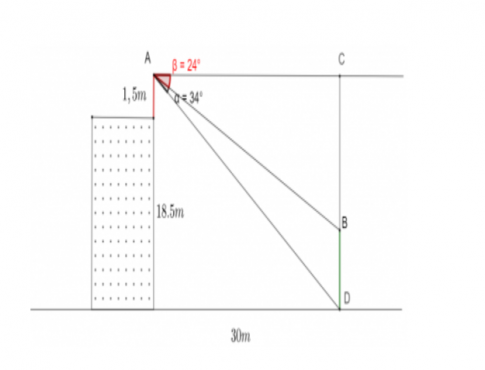
Gọi A là vị trí đặt mắt quan sát bằng giác kế, B là vị trí ngọn cây, D là vị trí gốc cây.

Gọi C là hình chiếu vuông góc của A lên BD.

+ Trường hợp 1: Cây cao hơn vị trí quan sát.

Gọi góc $\widehat{BAC}= \beta= 24^{\circ}, \widehat{DAC}= \alpha= 34^{\circ}$

Áp dụng định lí sin trong tam giác ABC:

$\frac{BC}{\sin \beta}= \frac{AC}{\sin B}$

Mà $\widehat{B}= 90^{\circ} - \beta= 66^{\circ}$

$\Rightarrow \frac{BC}{\sin 24^{\circ}}= \frac{30}{\sin 66^{\circ}}$

⇒ $BC≈13,4 (m)$

Vậy chiều cao của cây là: $BD=BC+CD≈13,4 +18,5+1,5=33,4 (m)$

+ Trường hợp 2: Cây thấp hơn vị trí quan sát. 

Gọi góc $\widehat{BAC}= \beta= 24^{\circ}, \widehat{DAC}= \alpha= 34^{\circ}$

Áp dụng định lí sin cho tam giác ABC: 

$\frac{BC}{\sin \beta}= \frac{AC}{\sin \widehat{ABC}}$

⇒ $BC≈13,4 (m)$

Vậy chiều cao của cây là: 

$BD=DC-BC≈18,5+1,5-13,4=6,6 (m)$

Ví dụ 8 (SGK -tr76)