BÀI 2. GIẢI TAM GIÁC. TÍNH DIỆN TÍCH TAM GIÁC

I. GIẢI TAM GIÁC

II. TÍNH DIỆN TÍCH TAM GIÁC

Bài 1: Cho tam giác ABC có AB=12; B=60^o; C=45^o. Tính diện tích của tam giác ABC

Giải nhanh:

III. ÁP DỤNG VÀO BÀI TOÁN THỰC TIỄN

Bài 1: Từ trên nóc của một tòa nhà cao 18,5m, bạn Nam quan sát một cái cây cách toà nhà 30m và dùng giác kế đo được góc lệch giữa phương quan sát gốc cây và phương nằm ngang là 34^o, góc lệch giữa phương quan sát ngọn cây và phương nằm ngang là 24^o. Biết chiều cao của chân giác kế là 1,5 m. Chiều cao của cái cây là bao nhiêu mét (làm tròn kết quả đến hàng phần mười)?

Giải nhanh:

Gọi A là vị trí đặt mắt quan sát bằng giác kế, B là vị trí ngọn cây, D là vị trí gốc cây, C là hình chiếu vuông góc của A lên BD.

+ Trường hợp 1: Cây cao hơn vị trí quan sát.

Gọi góc ,

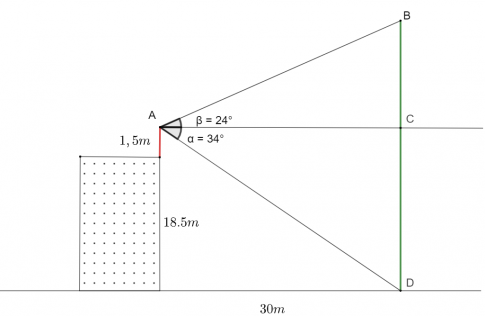
Áp dụng định lí sin trong tam giác ABC:

Mà

(m)

Vậy chiều cao của cây là: 

(m)

+ Trường hợp 2: Cây thấp hơn vị trí quan sát. 

Gọi ,

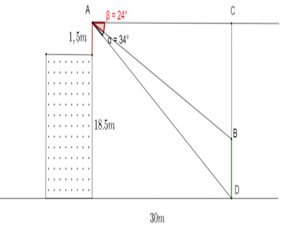
Áp dụng định lí sin cho tam giác ABC: 

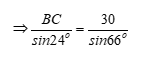
(m)

Vậy chiều cao của cây là: 

(m)

BÀI TẬP CUỐI SGK

Bài tập 1: Cho tam giác ABC có BC = 12, CA = 15, = 120^O. Tính:

a. Độ dài cạnh AB

b. Số đo các góc A,B

c. Diện tích tam giác ABC

Giải nhanh:

a. Áp dụng định lí côsin:

b. Áp dụng định lí sin:

c.

Bài tập 2: Cho tam giác ABC có AB = 5, BC = 7, = 120⁰. Tính độ dài cạnh AC

Giải nhanh:

Áp dụng định lí sin trong tam giác ABC:

Áp dụng định lí côsin:

Bài tập 3: Cho tam giác ABC có AB = 100, B = 100, = 45^O. Tính:

a. Độ dài các cạnh AC,BC

b. Diện tích tam giác ABC

Giải nhanh:

a. Ta có:

Áp dụng định lí sin:

+

+

b.

Bài tập 4: Cho tam giác ABC có AB = 12, AC = 15, BC = 20. Tính:

a. Số đo các góc A,B,C

b. Diện tích tam giác ABC

Giải nhanh:

a. Áp dụng định lí côsin:

b.

Bài tập 5: Tính độ dài cạnh AB trong mỗi trường hợp sau

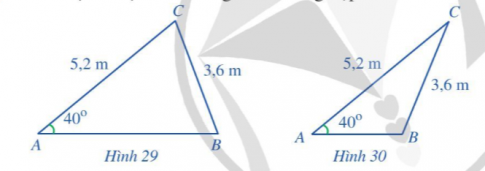
Giải nhanh:

Áp dụng định lí sin:

hoặc

+ Trường hợp 1: Với

Áp dụng định lí sin:

+ Trường hợp 2: Với

Áp dụng định lí sin:

Vậy  hoặc

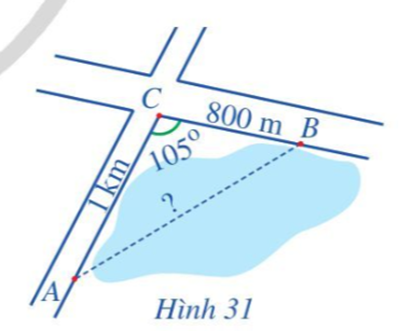
Bài tập 6: Để tính khoảng cách giữa hai địa điểm A và B mà ta không thể đi trực tiếp từ A đến B (hai địa điểm nằm ở hai bên bờ một hồ nước, một đầm lầy...), người ta tiến hành như sau: Chọn một địa điểm C sao cho ta đo được các khoảng cách AC,CB và góc ACB. Sau khi đo, ta nhận được: AC = 1 km, CB = 800 m và ACB = 105^O (Hình 31). Tính khoảng cách AB (làm tròn kết quả đến hàng phần mười theo đơn vị mét).

Giải nhanh:

AC1km = 1000 m

Áp dụng định lí cosin:  

Vậy khoảng cách ABC là 1433,2 m

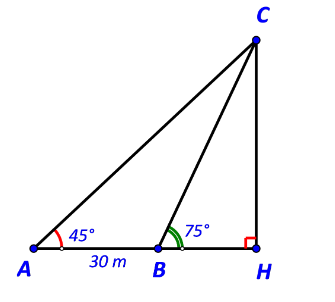
Bài tập 7:  Một người đi dọc bờ biển từ vị trí A đến vị trí B và quan sát một ngọn hải đăng. Góc nghiêng của phương quan sát từ các vị trí A,B tới ngọn hải đăng với đường đi của người quan sát là 45^O và 75^O. Biết khoảng cách giữa hai vị trí A,B là 30 m (Hình 32). Ngọn hải đăng cách bờ biển bao nhiêu mét (làm tròn kết quả đến hàng đơn vị)?

Giải nhanh:

Gọi C là vị trí ngọn hải đăng và H là hình chiếu vuông góc của C trên AB.

Khi đó CH là khoảng cách từ ngọn hải đăng tới bờ biển.

Ta có:,

Áp dụng định lí sin trong tam giác ABC:

Xét tam giác ACH có:

Vậy ngọn hải đăng cách bờ biển 41 m