Dễ hiểu giải Toán 10 Cánh diều bài 5 Phương trình đường tròn
Giải dễ hiểu bài 5 Phương trình đường tròn. Trình bày rất dễ hiểu, nên tiếp thu Toán 10 Cánh diều dễ dàng. Học sinh nắm được kiến thức và biết suy rộng ra các bài tương tự. Thêm 1 dạng giải mới để mở rộng tư duy. Danh mục các bài giải trình bày phía dưới
Nếu chưa hiểu - hãy xem: => Lời giải chi tiết ở đây
BÀI 5. PHƯƠNG TRÌNH ĐƯỜNG TRÒN
I. PHƯƠNG TRÌNH ĐƯỜNG TRÒN
Bài 1: Viết phương trình đường tròn tâm I(6;-4) đi qua điểm A(8;-7).
Giải nhanh:
![]()
Bài 2: Tìm k sao cho phương trình ![]() là phương trình đường tròn.
là phương trình đường tròn.
Giải nhanh:
![]()
![]()
![]()
Để phương trình là phương trình đường tròn ![]()
![]() ;
; ![]() .
.
Bài 3: Lập phương trình đường tròn đi qua ba điểm A(1;2); B(5;2); C(1;-3)
Giải nhanh:
![]()
II. PHƯƠNG TRÌNH TIẾP TUYẾN CỦA ĐƯỜNG TRÒN.
Bài 1: Lập phương trình tiếp tuyến tại điểm Mo(-1;-4) thuộc đường tròn ![]()
Giải nhanh:
Đường tròn tâm I(3; -7)
Phương trình tiếp tuyến tại điểm M(-1; -4) thuộc đường tròn ![]() là:
là:
(-1 – 3)(x + 1) + (-4 + 7)(y + 4) = 0 ![]() -4x + 3y + 8 = 0.
-4x + 3y + 8 = 0.
BAI TẬP CUỐI SGK
Bài tập 1: Phương trình nào sau đây là phương trình đường tròn ?
a. x2 + y2 – 2x + 2y – 7 = 0
b. x2 + y2 – 8x + 2y + 20 = 0
Giải nhanh:
a. x2 + y2 – 2x + 2y – 7 = 0 ![]()
![]()
Vậy phương trình x2 + y2 – 2x + 2y – 7 = 0 là phương trình đường tròn có tâm I(1; -1), bán kính R = 3.
b. x2 + y2 – 8x + 2y + 20 = 0 ![]() (vô lí).
(vô lí).
Vậy phương trình x2 + y2 – 8x + 2y + 20 = 0 không là phương trình đường tròn.
Bài tập 2: Tìm tâm và bán kính của đường tròn trong mỗi trường hợp sau:
a. Đường tròn có phương trình ![]()
b. Đường tròn có phương trình x2 + y2 – 6x – 2y -15 = 0
Giải nhanh:
a. Ta có: ![]()
Do đó, đường tròn đã cho có tâm I(-1; 5) và bán kính R = 3.
b. Ta có: x2 + y2 – 6x – 2y -15 = 0 ![]()
Do đó, đường tròn đã cho có tâm I(3; 1) và bán kính R = ![]() = 5.
= 5.
Bài tập 3: Lập phương trình đường tròn trong mỗi trường hợp sau:
a. Đường tròn có tâm O(-3;4) và bán kính R = 9
b. Đường tròn có tâm I(5;-2) và đi qua điểm M(4;-1)
c. Đường tròn có tâm I(1;-1) và có một tiếp tuyến là $\Delta :5x-12y-1=0$
d. Đường tròn đường kính AB với A(3;-4) và B(-1;6)
e. Đường tròn đi qua ba điểm A(1;1); B(3;1); C(0;4)
Giải nhanh:
a. ![]()
b. ![]()
c. Đường tròn có tâm I(1; -1) và có một tiếp tuyến là ![]()
![]() Đường tròn có bán kính R = d(I;
Đường tròn có bán kính R = d(I; ![]() ) =
) = ![]()
![]() Phương trình của đường tròn là:
Phương trình của đường tròn là:
![]()
d. Đường tròn đường kính AB với A(3; -4) và B(-1; 6) đi qua tâm I là trung điểm của AB.
![]() I(1; 1) và có bán kính R =
I(1; 1) và có bán kính R = ![]()
Có: ![]()
![]() Đường tròn có phương trình là:
Đường tròn có phương trình là: ![]()
e. Đường tròn đi qua ba điểm A(1; 1); B(3; 1); C(0; 4)
Giả sử tâm đường tròn là I(a; b). Ta có:
IA = IB = IC ![]() nên:
nên:
![]()
![]()
Đường tròn tâm I(2; 3) bán kính R = IC = ![]()
Vậy phương trình đường tròn là: ![]()
Bài tập 4: Lập phương trình tiếp tuyến tại điểm có hoành độ bằng 3 thuộc đường tròn: ![]()
Giải nhanh:
Ta có: ![]()
Do đó, đường tròn đã cho có tâm I(-2; -7) và bán kính R = 13.
Hoành độ của tiếp điểm là 3 hay x = 3, thay vào phương trình đường tròn ta được:
![]()
![]() y = 5 hoặc y = -19
y = 5 hoặc y = -19
Do đó ta tìm được các điểm thuộc đường tròn có hoành độ bằng 3 là: A(3; 5) và B(3; -19).
Phương trình tiếp tuyến của đường tròn tâm I(-2; -7) tại điểm A(3; 5) là:
(3 + 2)(x – 3) + (5 + 7)(y – 5) = 0 ![]() 5x + 12y – 75 = 0.
5x + 12y – 75 = 0.
Phương trình tiếp tuyến của đường tròn tâm I(-2; -7) tại điểm B(3; -19) là:
(3 + 2)(x – 3) + (-19 + 7)(y – (-19)) = 0 ![]() 5x - 12y – 243 = 0.
5x - 12y – 243 = 0.
Vậy các phương trình tiếp tuyến thỏa mãn là:
5x + 12y – 75 = 0
5x - 12y – 243 = 0
Bài tập 5: Tìm m sao cho đường thẳng 3x+4y+m=0 tiếp xúc với đường tròn: ![]()
Giải nhanh:
![]() : 3x + 4y + m = 0; (C):
: 3x + 4y + m = 0; (C): ![]()
Đường tròn (C) có tâm I(-1; 2), bán kính R = 2.
Vì ![]() là tiếp tuyến của đường tròn
là tiếp tuyến của đường tròn
![]() d(I;
d(I; ![]() ) = R
) = R ![]()
![]() m = 5 hoặc m = -15.
m = 5 hoặc m = -15.
Vậy m = 5 hoặc m = -15 thoả mãn yêu cầu
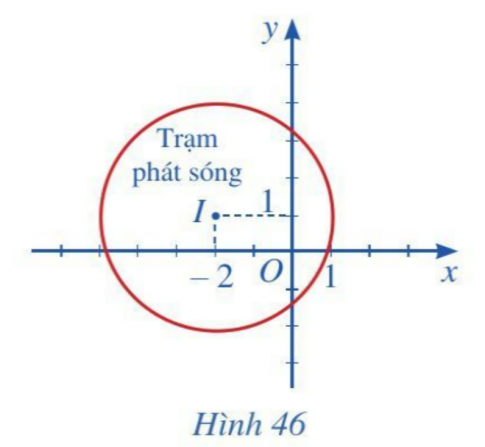
Bài tập 6: Hình 46 mô phỏng một trạm thu phát sóng điện thoại di động đặt ở vị trí I có toạ độ (– 2 ; 1) trong mặt phẳng toạ độ (đơn vị trên hai trục là ki-lô-mét).
Giải nhanh:
a. Đường tròn mô tả ranh giới bên ngoài của vùng phủ sóng có tâm I(-2 ; 1) và bán kính R = 3.
Vậy phương trình đường tròn cần lập là ![]()
b. Khoảng cách từ tâm I của đường tròn ranh giới tới vị trí có tọa độ M(-1 ; 3) là:
IM = ![]()
![]() Người dùng điện thoại ở vị trí có tọa độ (-1 ; 3) không thể sử dụng dịch vụ của trạm này.
Người dùng điện thoại ở vị trí có tọa độ (-1 ; 3) không thể sử dụng dịch vụ của trạm này.
c.
Giả sử vị trí đứng của người đó là B(-3 ; 4)
![]() Vectơ pháp tuyến của (BI) là :
Vectơ pháp tuyến của (BI) là : ![]()
![]() Phương trình tổng quát của (BI) : 3(x +2) + 1(y – 1) = 0 hay (BI) : 3x + y + 5 = 0.
Phương trình tổng quát của (BI) : 3(x +2) + 1(y – 1) = 0 hay (BI) : 3x + y + 5 = 0.
Gọi A là giao điểm của đường tròn tâm I và (BI) ![]() Khoảng cách ngắn nhất để người đó di chuyển được từ vị trí B(-3 ; 4) tới vùng phủ sóng là AB.
Khoảng cách ngắn nhất để người đó di chuyển được từ vị trí B(-3 ; 4) tới vùng phủ sóng là AB.
Toạ độ của A là nghiệm của hệ :
![]()
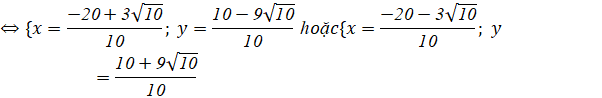
+ Với A![]()
Ta có: AB = ![]()
+ Với A![]()
Ta có: AB = ![]()
Do 0,2 < 6,2 nên ta chọn kết quả 0,2.
Vậy tính theo đường chim bay, khoảng cách ngắn nhất để một người ở vị trí có tọa độ (-3; 4) di chuyển được tới vùng phủ sóng là 0,2 km.
Bài tập 7: Ném đĩa là một môn thể thao thi đấu trong Thế vận hội Olympic mùa hè. Khi thực hiện cú ném, vận động viên thường quay lưng lại với hướng ném, sau đó xoay ngược chiều kim đồng hồ một vòng rưỡi của đường tròn để lấy đà rồi thả tay ra khỏi đĩa. Giả sử đĩa chuyển động trên một đường tròn tâm bán kính 0,8 trong mặt phẳng tọa độ Oxy (đơn vị trên hai trục là mét). Đến điểm , đĩa được ném đi (Hình 47). Trong những giây đầu tiên ngay sau khi được ném đi, quỹ đạo chuyển động của chiếc đĩa có phương trình như thế nào?
Giải nhanh:
Sau khi được ném đi, quỹ đạo chuyển động của chiếc đĩa nằm trên tiếp tuyến của đường tròn tâm I![]() tại điểm M
tại điểm M![]() .
.
Vậy quỹ đạo chuyển động của chiếc đĩa nằm trên đường thẳng có phương trình là:
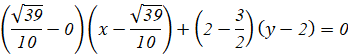
![]()
Nếu chưa hiểu - hãy xem: => Lời giải chi tiết ở đây

Bình luận