BÀI 3. PHƯƠNG TRÌNH ĐƯỜNG THẲNG

I. PHƯƠNG TRÌNH THAM SỐ CỦA ĐƯỜNG THẲNG

Bài 1: Cho đường thẳng Δ có phương trình tham số: x = 1 - 2t và y = -2 + t

a. Chỉ ra tọa độ của hai điểm thuộc đường thẳng Δ

b. Điểm nào trong các điểm C(-1;-1); D(1;3) thuộc đường thẳng Δ

Giải nhanh:

a. A M(1 – 2t; -2 + t) 

+ Chọn t = 1

+ Chọn t = 0

b. C(-1; -1) vào đường thẳng ta được:

Vậy C(-1; -1)

Thay toạ độ điểm D(1; 3) vào đường thẳng ta được:

Vậy D(1; 3)

II. PHƯƠNG TRÌNH TỔNG QUÁT CỦA ĐƯỜNG THẲNG

Bài 1: Cho đường thẳng Δ có phương trình tổng quát là x - y + 1 = 0

a. Chỉ ra tọa độ của một vectơ pháp tuyến và một vectơ chỉ phương của Δ

b. Chỉ ra tọa độ của hai điểm thuộc Δ

Giải nhanh:

a. ; .

b. Chọn x = 0, thay vào phương trình đường thẳng ta được: 

1 – y + 1 = 0 .

=> Điểm A(0; 2) thuộc đường thẳng .

Chọn x = 1, thay vào phương trình đường thẳng ta được: 

0 – y + 1 = 0 .

=> Điểm B(1; 1) thuộc đường thẳng

BÀI TẬP CUỐI SGK

Bài tập 1: Cho đường thẳng Δ có phương trình tổng quát của đường thẳng đi qua điểm A(-1;2) và 

a. Có vectơ pháp tuyến là =(3;2)

b. Có vectơ chỉ phương là =(−2;3)

Giải nhanh:

a. 3x + 2y – 1 = 0

b. x = -1 -2t và y = 2 + 3t (t là tham số)

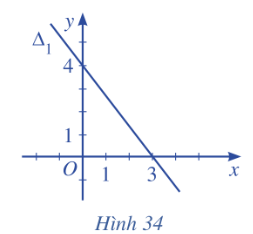
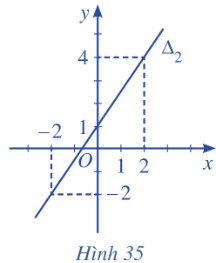
Bài tập 2: Lập phương trình mỗi đường thẳng trong các Hình 34, 35, 36, 37 sau đây:

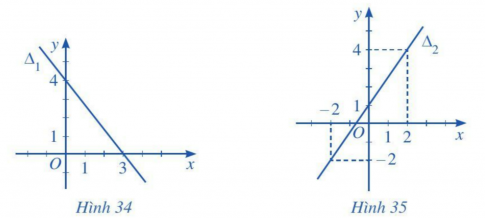
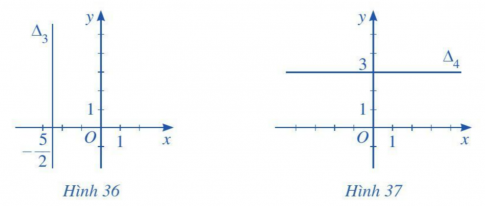
Giải nhanh:

Hình 34:

Hình 35:

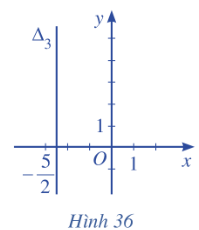
Hình 36: Do đường thẳng vuông góc với Ox nên vectơ pháp tuyến của là  

Phương trình đường thẳng đi qua điểm có vectơ pháp tuyến là: 

1

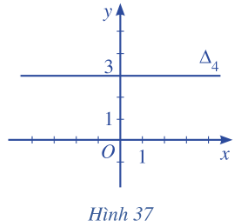
Hình 37: Do đường thẳng vuông góc với Ox nên vectơ pháp tuyến của là

Phương trình đường thẳng đi qua điểm (0; 3) có vectơ pháp tuyến là: 0(x – 0) + 1(y – 3) = 0 y = 3.

Bài tập 3: Cho đường thẳng d có phương trình tham số là:

x = -1 -3t và y = 2+ 2t

a. Lập phương trình tổng quát của đường thẳng d.

b. Tìm tọa độ giao điểm của đường thẳng d lần lượt với các trục Ox, Oy.

c.  Đường thẳng d có đi qua điểm M (-7; 5) hay không?

Giải nhanh:

a. Đường thẳng d đi qua A(-1; 2) nhận làm vectơ chỉ phương 

Phương trình tổng quát của đường thẳng d là:  2x + 3y – 4 = 0.

b. Xét hệ phương trình:

Vậy giao điểm d với trục Oy là: A

Xét hệ phương trình:

Vậy giao điểm d với trục Ox là: B(2; 0)

c. Thay toạ độ điểm M(-7; 5) vào phương trình đường thẳng d ta có: 

2.(-7) + 3.5 – 4 0.

Vậy M(-7; 5) không thuộc đường thẳng d.   

Bài tập 4: Cho đường thẳng d có phương trình tổng quát là: x - 2y - 5 = 0

a. Lập phương trình tham số của đường thẳng d.

b. Tìm tọa độ điểm M thuộc d sao cho OM = 5 với O là gốc tọa độ.

c. Tìm tọa độ điểm N thuộc d sao cho khoảng cách từ N đến trục hoành Ox là 3.

Giải nhanh:

(d): x – 2y – 5 =0

a. Ta có: ;

Chọn điểm A(1; -2) d. Vậy phương trình tham số của đường thẳng d là: 

 (t là tham số)

b. Do điểm M thuộc d nên ta có: M (1 + 2m; -2 + m); m

OM = 5

+ m = 2 M(5; 0)
+ m = -2 M(-3; -4)

c. n = 5 hoặc n = -1

+ n = 5 N(11; 3)

+ n = -1 N(-1; -3)

Bài tập 5: Cho tam giác ABC, biết A(1; 3); B(-1; -1); C(5; -3). Lập phương trình tổng quát của:

a. Ba đường thẳng AB, BC, AC.

b. Đường trung trực cạnh AB.

c. Đường cao AH và đường trung tuyến AM của tam giác ABC.

Giải nhanh:

A(1; 3), B(-1; -1), C (5; -3)

a. Phương trình đường thẳng AB đi qua hai điểm A và B là: 

Phương trình đường thẳng AC đi qua hai điểm A và C là:

Phương trình đường thẳng BC đi qua 2 điểm B và C là: 

b. Gọi d là trung trực của cạnh AB.

Lấy N là trung điểm của AB N(0; 1).

Do d AB nên ta có vectơ pháp tuyến của d là: = (1; 2).

Phương trình đường thẳng d đi qua N có vectơ pháp tuyến = (1; 2) là:

1(x – 0) + 2(y – 1)  = 0 x + 2y – 2 = 0 

c. + Do AH vuông góc với BC nên vectơ pháp tuyến của AH là = (3; -1)

Phương trình đường cao AH đi qua điểm A có vectơ pháp tuyến = (3; -1) là:

3(x – 1) – 1(y – 3) = 0 3x – y = 0

+ Do M là trung điểm của BC nên M(2; -2); = (1; 5) = (5; 1).

Phương trình trung tuyến AM đi qua điểm A có vectơ pháp tuyến = (5; 1) là:

5(x – 1) + 1(y – 3) = 0 5x + y – 8 = 0

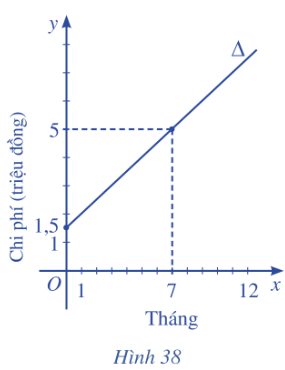
Bài tập 6: Để tham gia một phòng tập  thể dục, người tập phải trả một khoản phí tham gia ban đầu và phí sử dụng phòng tập. Đường thẳng $\Delta$ ở Hình 38 biểu thị tổng chi phí (đơn vị: triệu đồng) để tham gia một phòng tập thể dục theo thời gian tập của một người (đơn vị: tháng)

Giải nhanh:

a. Đường thẳng đi qua hai điểm lần lượt có toạ độ (0 ; 1,5), (7 ; 5) nên có phương trình là:

b. Giao điểm của đường thẳng với trục Oy ứng với x = 0. Thời điểm x = 0 cho biết khoản phí tham gia ban đầu mà người tập phải trả. Khi x = 0 thì y = 1,5, vì vậy khoản phí tham gia ban đầu mà người tập phải trả là 1 500 000 đồng.

c. Thay x = 12 vào đường thẳng ta có : y =7,5

Vậy tổng chi phí mà người đó phải trả khi tham gia phòng tập thể dục trong 12 tháng là 7,5 triệu đồng.