Dễ hiểu giải Toán 10 Cánh diều bài 6 Tích vô hướng của hai vectơ
Giải dễ hiểu bài 6 Tích vô hướng của hai vectơ. Trình bày rất dễ hiểu, nên tiếp thu Toán 10 Cánh diều dễ dàng. Học sinh nắm được kiến thức và biết suy rộng ra các bài tương tự. Thêm 1 dạng giải mới để mở rộng tư duy. Danh mục các bài giải trình bày phía dưới
Nếu chưa hiểu - hãy xem: => Lời giải chi tiết ở đây
BÀI 6. TÍCH VÔ HƯỚNG CỦA HAI VECTƠ
I. ĐỊNH NGHĨA
Bài 1: Cho tam giác ABC vuông tại A có B = 300, AB = 3cm. Tính 
Giải nhanh:
+ 
.
= 3.2
.cos300 = 9
+ 
.
= 
.2
.cos600 = 3
Bài 2: Cho tam giác ABC đều cạnh a, AH là đường cao. Tính:
a) 
.
b) 
.
Giải nhanh:
a) 
.
= 
b) 
.
= 0
II. TÍNH CHẤT
Bài 1: Chứng minh rằng với hai vectơ bất kì 
, ta có:
+ 
+ 
Giải nhanh:
+ 
+ 
+ 
III. MỘT SỐ ỨNG DỤNG
Bài 1: Sử dụng tích vô hướng, chứng minh định lí Pythagore: Tam giác ABC vuông tại A khi và chỉ khi BC2 = AB2 + AC2
Giải nhanh:
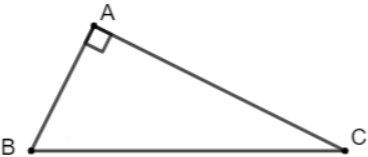
Do tam giác ABC vuông tại A nên 
Ta có:
Vậy BC2 = AB2 + AC2 (đpcm)
Ta có:
Mà theo giả thiết ta có:
BC2 = AB2 + AC2
hay cos
Do đó 
= 
Vậy tam giác ABC vuông tại A (đpcm)
BÀI TẬP CUỐI SGK
Bài tập 1: Nếu hai điểm M, N thỏa mãn 
. 
= -4 thì độ dài đoạn thẳng MN bằng bao nhiêu?
A. MN = 4
B. MN = 2
C. MN = 16
D. MN = 256
Giải nhanh:
B. MN = 2
Bài tập 2: Phát biểu nào sau đây là đúng ?
A. Nếu 
khác 
và (
) < 900 thì 
< 0
B. Nếu 
khác 
và (
) > 900 thì 
> 0
C. Nếu 
khác 
và (
) < 900 thì 
> 0
D. Nếu 
khác 
và (
) ≠ 900 thì 
< 0
Giải nhanh:
C. Nếu 
khác 
và (
) < 900 thì 
> 0
Bài tập 3: Tính 
trong mỗi trường hợp sau:
a) 
; 
= 300
b) 
; 
= 1200
c) 
; 
cùng hướng
d) 
; 
ngược hướng
Giải nhanh:
a. 
b. 
5.6.
c. 
2.3.
d. 
2.3.
Bài tập 4: Cho hình vuông ABCD cạnh a. Tính các tích vô hướng sau:
a) 
b) 
Giải nhanh:
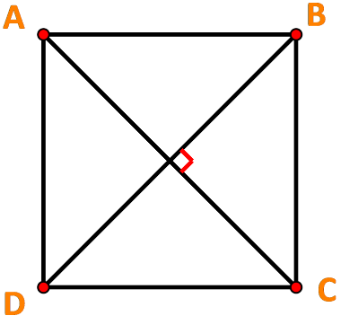
a. 
b. 
Bài tập 5: Cho tam giác ABC. Chứng minh: 
0
Giải nhanh:
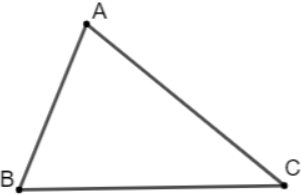
(đpcm)
Bài tập 6: Cho tam giác nhọn ABC, kẻ đường cao AH. Chứng minh rằng:
a) 
b) 
Giải nhanh:
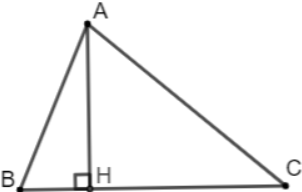
a. 
b. 
Bài tập 7: Một máy bay đang bay từ hướng đông sang hướng tây với tốc độ 700 km/h thì gặp luồng gió thổi từ hướng đông bắc sang hướng tây nam với tốc độ 40 km/h (Hình 68). Máy bay bị thay đổi vận tốc sau khi gặp gió thổi.Tìm tốc độ mới của máy bay (làm tròn kết quả đến hàng phần trăm theo đơn vị km/h).
Giải nhanh:
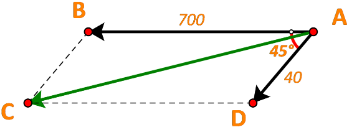
(km/h)
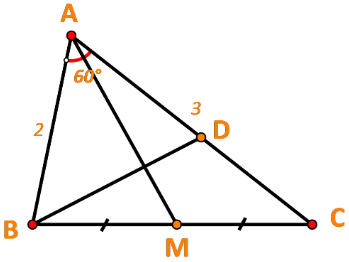
Bài tập 8: Cho tam giác ABC có AB = 2, AC = 3, 
= 600. Gọi M là trung điểm của đoạn thẳng BC. Điểm D thỏa mãn 
Tính
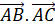
Biểu diễn
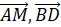theo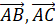 
Chứng minh AM ⊥ BD
Giải nhanh:
a. 
b. 
)
c. 
Như vậy AM 
BD
Nếu chưa hiểu - hãy xem: => Lời giải chi tiết ở đây
Nội dung quan tâm khác
Thêm kiến thức môn học
Giải bài tập những môn khác
Giải SGK 10 KNTT
Giải SGK 10 CTST
Giải SGK 10 Cánh diều
Giải SBT lớp 10 kết nối tri thức
Giải SBT lớp 10 chân trời sáng tạo
Giải SBT lớp 10 Cánh diều
Giải chuyên đề học tập 10 Kết nối tri thức
Giải chuyên đề học tập 10 Chân trời sáng tạo
Giải chuyên đề học tập 10 Cánh diều
Trắc nghiệm 10 Kết nối tri thức
Trắc nghiệm 10 Chân trời sáng tạo
Trắc nghiệm 10 Cánh diều
Bình luận