I. ĐỊNH NGHĨA

1. Tích vô hướng của hai vectơ có cùng điểm đầu

Trong mặt phẳng, cho hai vectơ $\overrightarrow{OA}, \overrightarrow{OB}$ khác $\overrightarrow{0}.$

Kết luận:

+ Góc giữa hai vectơ $\overrightarrow{OA}, \overrightarrow{OB}$ là góc giữa hai tia $OA, OB$ và được kí hiệu là $(\overrightarrow{OA}, \overrightarrow{OB}).$

+ Tích vô hướng của hai vectơ $\overrightarrow{OA}$ và $\overrightarrow{OB}$ là một số, kí hiệu $\overrightarrow{OA}, \overrightarrow{OB}$, được xác định bởi công thức: $\overrightarrow{OA}.\overrightarrow{OB}= \left | \overrightarrow{OA} \right |.\left | \overrightarrow{OB} \right |.\cos(\overrightarrow{OA}, \overrightarrow{OB})$

Ví dụ 1 (SGK – tr93) 

Luyện tập 1:

Ta có: $AC = AB.\tan 30^{\circ} = 3; BC = \frac{AB}{\cos 30^{\circ}}= 2\sqrt{3}$

+ $\overrightarrow{BA}.\overrightarrow{BC}= \left | \overrightarrow{BA} \right |.\left | \overrightarrow{BC} \right |.\cos(\overrightarrow{BA}, \overrightarrow{BC})= 3.2\sqrt3.\cos 30^{\circ} = 9$

+ $\overrightarrow{CA}.\overrightarrow{CB}= \left | \overrightarrow{CA} \right |.\left | \overrightarrow{CB} \right |.\cos(\overrightarrow{CA}, \overrightarrow{CB})= \sqrt3.2\sqrt3.\cos 60^{\circ} = 3$

2. Tích vô hướng của hai vectơ tuỳ ý 

Cho hai vectơ $\overrightarrow{a}$ và $\overrightarrow{b}$ khác $\overrightarrow{0}$. Lấy điểm O và vẽ vectơ $\overrightarrow{OA}= \overrightarrow{a}$ và $\overrightarrow{OB}= \overrightarrow{b}.$

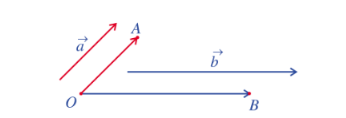
Kết luận:

+ Góc giữa hai vectơ $\overrightarrow{a}, \overrightarrow{b},$ kí hiệu $(\overrightarrow{a},\overrightarrow{b})$, là góc giữa hai vectơ $\overrightarrow{OA}, \overrightarrow{OB}$

+ Tích vô hướng của hai vectơ $\overrightarrow{a}$ và $\overrightarrow{b}$, kí hiệu $\overrightarrow{a}, \overrightarrow{b},$ là tích vô hướng cùa hai vectơ $\overrightarrow{OA}$ và $\overrightarrow{OB}$. Như vậy, tích vô hướng của hai vectơ $\overrightarrow{a}$ và $\overrightarrow{b}$ là một số thực được xác định bởi công thức: $\overrightarrow{a}.\overrightarrow{b}= \left | \overrightarrow{a} \right |.\left | \overrightarrow{b} \right |.\cos(\overrightarrow{a}, \overrightarrow{b})$

Quy ước: 

Tích vô hướng của một vectơ bất kì với vectơ $\overrightarrow{0}$ là số 0. 

Chú ý: 

+ $(\overrightarrow{a},\overrightarrow{b})= (\overrightarrow{b},\overrightarrow{a})$

+ Nếu $(\overrightarrow{a},\overrightarrow{b})= 90^{\circ}$ thì ta nói hai vectơ $\overrightarrow{a},\overrightarrow{b}$ vuông góc với nhau, kí hiệu $\overrightarrow{a} \perp \overrightarrow{b}$ hoặc $\overrightarrow{b} \perp \overrightarrow{a}.$ Khi đó $\overrightarrow{a}.\overrightarrow{b}= \left | \overrightarrow{a} \right |.\left | \overrightarrow{b} \right |.\cos 90^{\circ} = 0$

+ Tích vô hướng của hai vectơ cùng hướng bằng tích hai độ dài của chúng. 

+ Tích vô hướng của hai vectơ ngược hướng bằng số đối của tích hai độ dài của chúng. 

Ta có thể chứng minh chú ý thứ ba như sau: 

Nếu $\overrightarrow{a}, \overrightarrow{b}$ là hai vectơ (khác $\overrightarrow{0}$) cùng hướng thì $(\overrightarrow{a}, \overrightarrow{b})= 0^{\circ}$. Do đó, $\cos (\overrightarrow{a}, \overrightarrow{b}) = 1.$ 

Vì vậy, $\overrightarrow{a}.\overrightarrow{b}= \left | \overrightarrow{a} \right |.\left | \overrightarrow{b} \right |.\cos (\overrightarrow{a},\overrightarrow{b})= \left | \overrightarrow{a} \right |.\left | \overrightarrow{b} \right |$

Nếu một trong hai vectơ $\overrightarrow{a}, \overrightarrow{b}$ là vectơ $\overrightarrow{0}$ thì $\overrightarrow{a}.\overrightarrow{b}= 0$ và $\overrightarrow{a}. \overrightarrow{b}= 0$ nên $\overrightarrow{a}. \overrightarrow{b}= \left | \overrightarrow{a} \right |.\left | \overrightarrow{b} \right |$

Chú ý thứ tư được chứng minh tương tự như trên. 

Ví dụ 2 (SGK – tr94)

Luyện tập 2:

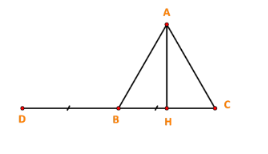
a. Vẽ vectơ $\overrightarrow{BD}= \overrightarrow{CB}$. Ta có:

$(\overrightarrow{CB}, \overrightarrow{BA})= (\overrightarrow{BD}, \overrightarrow{BA})= \widehat{DBA}= 120^{\circ}$

Vậy $\overrightarrow{CB}. \overrightarrow{BA}= a.a. \cos 120^{\circ}= \frac{-a^2}{2}.$

Vì $AH \perp BC$ nên $\overrightarrow{AH}. \overrightarrow{BC}= 0.$

II. TÍNH CHẤT 

Kết luận: 

Với hai vectơ bất kì $\overrightarrow{a}, \overrightarrow{b}$ và số thực $k$ tuỳ ý, ta có: 

• $\overrightarrow{a}.\overrightarrow{b}= \overrightarrow{b}.\overrightarrow{a}$ (tính chất giao hoán)

• $\overrightarrow{a}.(\overrightarrow{b}+\overrightarrow{c})= \overrightarrow{a}.\overrightarrow{b}+\overrightarrow{a}.\overrightarrow{c}$ (tính chất phân phối)

• $(k\overrightarrow{a}).\overrightarrow{b}= k(\overrightarrow{a}.\overrightarrow{b})= \overrightarrow{a}.(k\overrightarrow{b})$

• $\overrightarrow{a}^2 ≥ 0, \overrightarrow{a}^2 = 0 ⟺ \overrightarrow{a}= \overrightarrow{0}$

Trong đó, kí hiệu $\overrightarrow{a}.\overrightarrow{a}= \overrightarrow{a}^2$ và biểu thức này được gọi là bình phương vô hướng của vectơ $\overrightarrow{a}$.

Ví dụ 3, 4 (SGK – tr95)

Luyện tập 3:

•  $(\overrightarrow{a}+ \overrightarrow{b})^2= (\overrightarrow{a}+ \overrightarrow{b}). (\overrightarrow{a}+ \overrightarrow{b})$= $\overrightarrow{a}.\overrightarrow{a}+ \overrightarrow{b}. \overrightarrow{a}+ \overrightarrow{a}.\overrightarrow{b} + \overrightarrow{b}. \overrightarrow{b}$

= $\overrightarrow{a}^2 + 2\overrightarrow{a}.\overrightarrow{b} + \overrightarrow{b}^2$

•  $(\overrightarrow{a}-\overrightarrow{b})^2= (\overrightarrow{a}-\overrightarrow{b}).(\overrightarrow{a}-\overrightarrow{b})$= $\overrightarrow{a}.\overrightarrow{a} - \overrightarrow{b}.\overrightarrow{a} - \overrightarrow{a}.{b}+ \overrightarrow{b}.\overrightarrow{b}$

= $\overrightarrow{a}^2 - 2\overrightarrow{a}.\overrightarrow{b} + \overrightarrow{b}^2$

•  $(\overrightarrow{a}-\overrightarrow{b}).(\overrightarrow{a}+\overrightarrow{b})$= $\overrightarrow{a}.\overrightarrow{a}- \overrightarrow{b}.\overrightarrow{a}+ \overrightarrow{a}.\overrightarrow{b} - \overrightarrow{b}.\overrightarrow{b}$

= $\overrightarrow{a}^2 - \overrightarrow{b}^2$

III. MỘT SỐ ỨNG DỤNG 

1. Tính độ dài của đoạn thẳng

Nhận xét: 

Với hai điểm $A, B$ phân biệt, ta có: $\overrightarrow{AB}^2= \left | \overrightarrow{AB} \right |^2$

Do đó độ dài đoạn thẳng AB được tính như sau: $AB = \sqrt{\overrightarrow{AB}^2}$

Ví dụ 5 (SGK – tr96)

Luyện tập 4: 

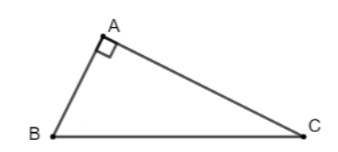
+ Cho tam giác ABC vuông tại A, ta chứng minh $BC^2 = AB^2 + AC^2$

Do tam giác $ABC$ vuông tại A nên $AC ⊥ AB ⇒ \cos (\overrightarrow{AB}, \overrightarrow{AC})= 0$

Ta có: 

$\overrightarrow{BC}^2= (\overrightarrow{AC}- \overrightarrow{AB})^2= \overrightarrow{AC}^2+ \overrightarrow{AB}^2 - 2\overrightarrow{AC}.\overrightarrow{AB}$ 

$\Rightarrow \overrightarrow{BC}^2= \overrightarrow{AC}^2 - 2.AC.AB. \cos (\overrightarrow{AC},\overrightarrow{AB})+ AB^2$

= $AC^2+ AB^2 - 2AC.AB. \cos90^{\circ}= AC^2+ AB^2.$ 

Vậy $BC^2 = AB^2 + AC^2$ (đpcm)

+ Cho tam giác ABC có $BC^2 = AB^2 + AC^2,$ cần chứng minh tam giác ABC vuông tại A. 

Ta có:

$\overrightarrow{BC}^2= (\overrightarrow{AC}- \overrightarrow{AB})^2= \overrightarrow{AC}^2+ \overrightarrow{AB}^2 - 2\overrightarrow{AC}.\overrightarrow{AB}$ 

$\Rightarrow BC^2= AC^2 - 2.AC.AB. \cos (\overrightarrow{AC}, \overrightarrow{AB})+ AB^2$ 

Mà theo giả thiết ta có: 

$BC^2= AB^2 + AC^2$

=> $BC^2= BC^2 - 2.AC.AB. \cos (\overrightarrow{AC},\overrightarrow{AB})$

=> $\cos (\overrightarrow{AC}, \overrightarrow{AB})= 0$ hay $\cos \widehat{BAC}= 0$

Do đó $\widehat {BAC}= 90^{\circ}$

Vậy tam giác $ABC$ vuông tại A (đpcm).

2. Chứng minh hai đường thẳng vuông góc

Nhận xét: 

Cho hai vectơ bất kì $\overrightarrow{a}$ và $\overrightarrow{b}$ khác vectơ $\overrightarrow{0}$. Ta có: $\overrightarrow{a}.\overrightarrow{b}= 0 ⇔ \overrightarrow{a} \perp \overrightarrow{b}.$

Ví dụ 6 (SGK – tr97)