BÀI 2. BIỂU THỨC TỌA ĐỘ CỦA CÁC PHÉP TOÁN VECTƠ

I. BIỂU THỨC TOẠ ĐỘ CỦA PHÉP CỘNG HAI VECTƠ, PHÉP TRỪ HAI VECTƠ, PHÉP NHÂN MỘT SỐ VỚI MỘT VECTƠ. 

Bài 1: a. Cho . Tìm tọa độ của vectơ

a. Cho . Tìm tọa độ của vectơ

Giải nhanh:

a.

b. Ta có: = nên

Bài 2: Trong bài toán mở đầu, hãy tìm tọa độ của máy bay trực thăng tại thời điểm sau khi xuất phát 2 giờ.

Giải nhanh: 

Gọi C ( là vị trí máy bay trực thăng tại thời điểm sau khi xuất phát 2 giờ Ta có: .

Mà

II. TOẠ ĐỘ TRUNG ĐIỂM CỦA ĐOẠN THẲNG VÀ TỌA ĐỘ TRỌNG TÂM TAM GIÁC

Bài 1: Cho hai điểm A (2; 4)  và M(5; 7).Tìm tọa độ điểm B sao cho M là trung điểm đoạn thẳng AB.

Giải nhanh:

Gọi điểm B(x_B; y_B).

Vì M là trung điểm của AB nên x_M = ;

Vậy điểm B có toạ độ là B(8; 10)

Bài 2: Cho ba điểm A(-1;1); B(1;5); G(1;2).

a. Chứng minh ba điểm A, B, G không thẳng hàng.

b. Tìm tọa độ điểm C sao cho G là trọng tâm của tam giác ABC.

Giải nhanh:

a.

Vì nên

=> A, B, G không thẳng hàng

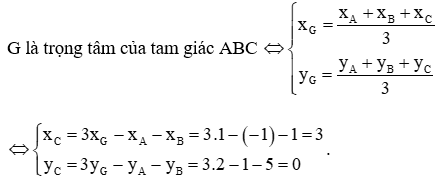
Vậy tọa độ điểm C là C(3; 0)

III. BIỂU THỨC TOẠ ĐỘ CỦA TÍCH VÔ HƯỚNG

BÀI TẬP CUỐI SGK

Bài tập 1: Trong mặt phẳng tọa độ Oxy, cho  , ,

a. Tìm tọa độ vectơ sao cho =

b. Tìm tọa độ vectơ sao cho +

Giải nhanh:

a. = [2.(-1) + 3 – 3.2; 2.2 + 1 – 3.(-3)]  = (-5; 14)
b.

Vậy

Bài tập 2: Trong mặt phẳng tọa độ Oxy, cho A(-2; 3) ; B(4; 5); C(2; -3)

a. Chứng minh ba điểm A, B, C không thẳng hàng.

b. Tìm tọa độ trọng tâm G của tam giác ABC.

c. Giải tam giác ABC (làm tròn các kết quả đến hàng đơn vị).

Giải nhanh:

a. Ta có: , .

Vì nên

=> A, B, C không thẳng hàng. 

b. Do G là trọng tâm tam giác ABC nên:

Vậy G(

c. Ta có: , ,

AB =

Ta có: 

cos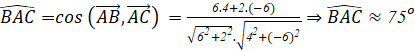

cos

Áp dụng định lí tổng ba góc trong một tam giác ta có:

Bài tập 3: Trong mặt phẳng tọa độ Oxy, cho tam giác ABC có trung điểm các cạnh BC, CA, AB tương ứng là M(2;0); N(4;2); P(1;3)

a. Tìm tọa độ các điểm A, B, C.

b. Trọng tâm hai tam giác ABC và MNP có trùng nhau không? Vì sao?

Giải nhanh:

a. Do M, N, P là trung điểm của các cạnh BC, CA, AB nên:

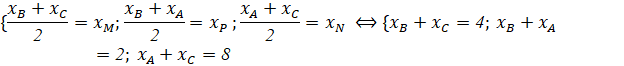
Vậy A (3; 5), B (-1 ; -1), C (5; -1). 

b. Trọng tâm tam giác ABC có tọa độ là:

Trọng tâm tam giác MNP có toạ độ là:

Vậy trọng tâm của 2 tam giác ABC và MNP là trùng nhau vì có cùng tọa độ.

Bài tập 4: Trong mặt phẳng tọa độ Oxy, cho tam giác ABC có A(2; 4); B(-1; 1); C(-8;2).

a. Tính số đo góc ABC (làm tròn kết quả đến hàng đơn vị theo đơn vị độ)

b. Tính chu vi của tam giác ABC.

c. Tìm tọa độ điểm M trên đường thẳng BC sao cho diện tích của tam giác ABC bằng hai lần diện tích của tam giác ABM.

Giải nhanh:

a. Ta có: ,

cos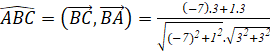

b. Ta có: , ,

AB =

BC =

Vậy chu vi tam giác ABC là: P_ABC = 2

c. Kẻ đường cao AH của tam giác ABC, M thuộc đường thẳng BC nên đường cao của tam giác ABM cũng là AH. 

Khi đó: và

Theo bài ra ta có:

. 

Vậy toạ độ điểm M là: . Vậy M

Bài tập 5: Cho ba điểm A(1; 1) ; B(4; 3) và C (6; -2)

a. Chứng minh ba điểm A, B, C không thẳng hàng.

b. Tìm tọa độ điểm D sao cho tứ giác ABCD là hình thang có AB//CD và CD = 2AB.

Giải nhanh:

a.

=> A, B, C không thẳng hàng.

b. A(1; 1), B(4; 3) và C(6; -2)

Ta có: ;

Vì hình thang ABCD có AB // CD nên hai vectơ , cùng hướng và CD = 2AB nên

Vậy toạ độ điểm D là D(0; -6).

Bài tập 6: Chứng minh khẳng định sau cùng phương khi và chỉ khi có một số thực k sao cho

Giải nhanh:

(0) cùng phương thì phải tồn tại một số k (k ) sao cho:

Bài tập 7: Một vật đồng thời bị ba lực tác động: lực tác động thứ nhất có độ lớn là 1500 N, lực tác động thứ hai có độ lớn là 600N, lực tác động thứ ba có độ lớn là 800N. Các lực này được biểu diễn bằng những vecto như Hình 23, với  ( (; (.Tính độ lớn lực tổng hợp tác động lên vật (làm tròn kết quả đến hàng đơn vị.

Giải nhanh:

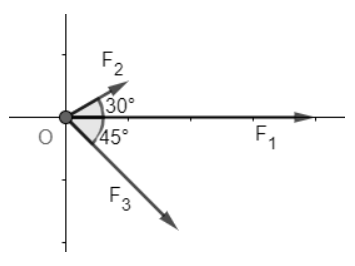
Chọn hệ trục toạ độ Oxy như hình vẽ. 

Ta có : + ( nên toạ độ của là: 

+ ( nên toạ độ của là: