BÀI 2. HÀM SỐ BẬC HAI. ĐỒ THỊ HÀM SỐ BẬC HAI VÀ ỨNG DỤNG

I. HÀM SỐ BẬC HAI 

Bài 1: Cho hai ví dụ về hàm số bậc 2.

Giải nhanh:

y = 3x² – 6x + 2

y = -5x² + 4

II. ĐỒ THỊ HÀM SỐ BẬC HAI

Bài 1: Vẽ đồ thị mỗi hàm số bậc hai sau:

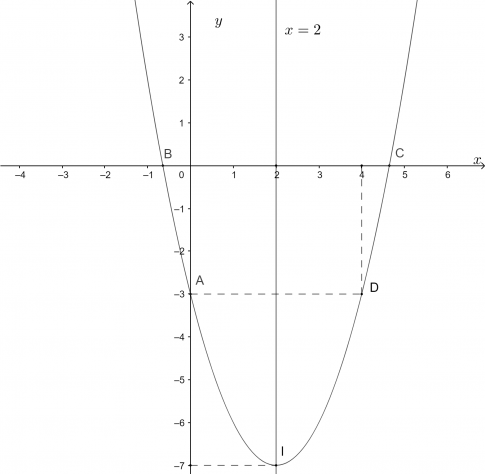
a. y = x² – 4x - 3

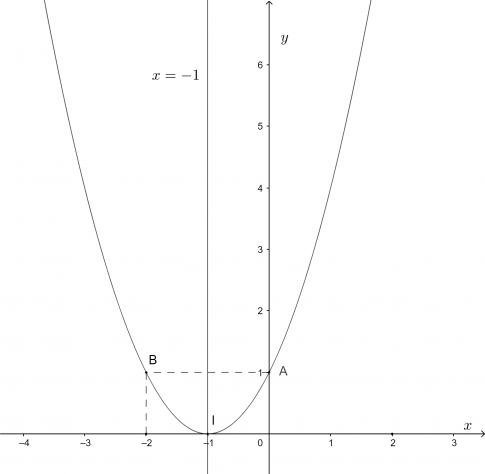
b. y = x² + 2x + 1

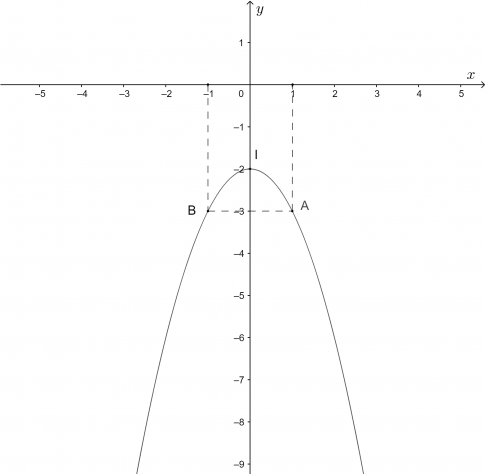
c. y = -x² – 2

Giải nhanh:

a. 

b.

c.

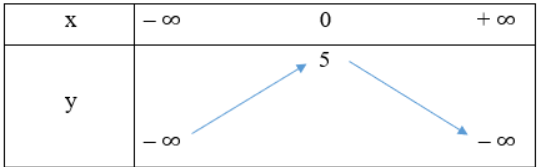
Bài 2: Lập bảng biến thiên của mỗi hàm số sau:

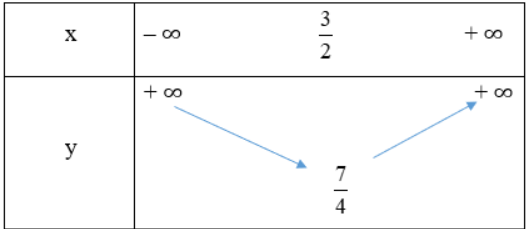
a. y = x² – 3x + 4

b. y = -2x² + 5

Giải nhanh:

a. Ta có: a = 1 > 0, b = -3, c = 4, = -7, = , =

  Hàm số nghịch biến trên khoảng (-; ) và đồng biến trên (;+)

b. Ta có: a = -2 < 0, b = 0, c = 5, = 40, = 0, = 5.

Hàm số đồng biến trên khoảng (-;0) và nghịch biến trên (0;+)

Ta có bảng biến thiên:

III. ỨNG DỤNG

Bài 1: Trong bài toán ở phần mở đầu, độ cao y(m) của một điểm thuộc vòng cung thành cầu cảng Sydney đạt giá trị lớn nhất là bao nhiêu mét (làm tròn kết quả đến hàng phần mười)?

Giải nhanh:

Ta có: (x – 251,5)² 0

-0,00188(x – 251,5)² + 118 118

Vậy y_max = 118 (m)

BÀI TẬP CUỐI SGK

Bài tập 1:  Trong các hàm số sau, hàm số nào là hàm số bậc hai? Với những hàm số bậc hai đó, xác định a,b,c lần lượt là hệ số của x², hệ số của x và hệ số tự do.

a. y = -3x²

b. y = 2x(x² – 6x +1)

c. y = 4x(2x – 5)

Giải nhanh:

a. y = -3x² là hàm số bậc hai 

a = -3; b = 0; c = 0

b. y = 2x(x² – 6x +1) không phải hàm số bậc hai

c. y = 4x(2x – 5) là hàm số bậc hai 

a = 8; b = -20; c = 0

Bài tập 2:  Xác định parabol y=ax²+bx+4 trong mỗi trường hợp sau:

a. Đi qua điểm M(1;12) và N(−3;4)

b. Có đỉnh là I(−3;−5)

Giải nhanh:

a. Parabol y = ax² + bx + 4 đi qua điểm M(1;12) và N(-3;4) nên ta có:

Vậy parabol là y = 2x² + 6x + 4

b. Ta có:  = -3 b = 6a (1)

Thay toạ độ I(-3;-5) vào y = ax² + bx + 4 ta được:

a.(-3)² + b.(-3) + 4 = -5 3a – b = -3 (2)

Từ (1) và (2) ta được

Vậy parabol là y = x² + 6x + 4.

Bài tập 3: Vẽ đồ thị của mỗi hàm số sau:

a. y = 2x² – 6x + 4

b. y = -3x² – 6x – 3

Giải nhanh:

a. y = 2x² – 6x + 4

Ta có: = (-6)² -4.2.4 = 4 

Đỉnh I

Trục đối xứng x =

Giao điểm của parabol với trục tung là A(0;4)

Giao điểm của parabol với trục hoành là B(1;0) và C(2;0)

Điểm đối xứng với điểm A(0;4) qua trục đối xứng x = là D(3;4) 

Do a > 0 nên đồ thị có bề lõm hướng lên trên

Vẽ parabol đi qua các điểm được xác định ở trên, ta nhận được đồ thị hàm số như hình: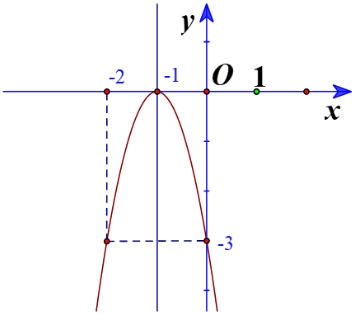

b. y = -3x² – 6x – 3

Ta có: = (-6)² – 4.(-3).(-3) = 0

Đỉnh I(-1;0)

Trục đối xứng x = -1

Giao điểm của parabol với trục tung là (0;-3)

Điểm đối xứng với điểm (0;-3) qua trục đối xứng x = -1 là (-2;-3)

Vẽ parabol đi qua các điểm được xác định ở trên, ta nhận được đồ thị hàm số: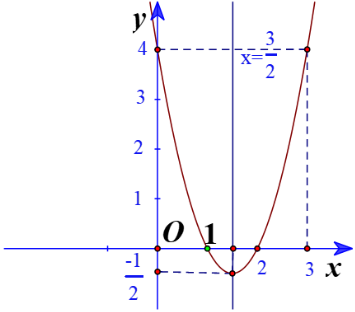

Bài tập 4: Cho đồ thị hàm số bậc hai ở Hình 15.

a. Xác định trục đối xứng, tọa độ đỉnh của đồ thị hàm số.

b. Xác định khoảng đồng biến, khoảng nghịch biến của hàm số.

c. Tìm công thức xác định hàm số.

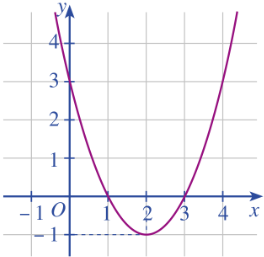
Giải nhanh:

a. Trục đối xứng là đường thẳng x = 2

Đỉnh I(2;-1)

b. Đồ thị hàm số nghịch biến trên khoảng (-;2) và đồng biến trên khoảng (2;+)

c. Gọi hàm số là y = ax² + bx + c (a0)

Ta có I(2;-1) nên  

Từ hình vẽ, ta có điểm (1;0) thuộc đồ thị nên: a + b + c = 0

Vậy parabol là y = x² – 4x + 3

Bài tập 5: Nêu khoảng đồng biến, khoảng nghịch biến của mỗi hàm số sau:

a. y = 5x² + 4x – 1 

b. y = -2x² + 8x + 6

Giải nhanh:

a. y = 5x² + 4x – 1 nghịch biến trên khoảng và đồng biến trên khoảng

b. y = -2x² + 8x + 6 đồng biến trên khoảng và nghịch biến trên khoảng

Bài tập 6: Khi du lịch đến thành phố St. Louis (Mỹ), ta sẽ thấy một cái cổng lớn có hình parabol hướng bề lõm xuống dưới, đó là cổng Arch. Giả sử ta lập một hệ tọa độ Oxy sao cho một chân cổng đi qua gốc O như Hình 16 ( x và y tính bằng mét), chân kia của cổng ở vị trí có tọa độ (162;0). Biết một điểm M trên cổng có toạ độ là (10;43). Tính chiều cao của cổng (tính từ điểm cao nhất trên cổng xuống mặt đất), làm tròn kết quả đến hàng đơn vị.

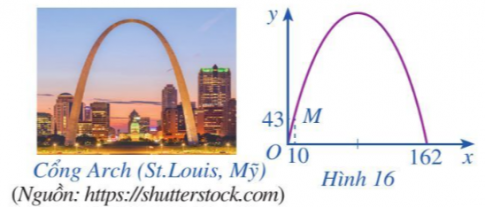
Giải nhanh:

Giả sử hàm số có dạng : y = ax² + bx + c (a < 0)

Ta có (0;0), (10;43), (162;0) thuộc đồ thị hàm số nên ta có :

Hoành độ đỉnh của đồ thị là : x = = 81 .

 Vậy chiều cao của cổng là 186m.