BÀI 6. BA ĐƯỜNG CONIC

I. ĐƯỜNG ELIP

Bài 1: Lập phương trình chính tắc của Elip (E) đi qua hai điểm M(0; 3) và N(3; -) 

Giải nhanh:

Elip có phương trình chính tắc là:

(a > b > 0)

Do M(0; 3) (E) nên:

  (1)

Do N(3; -) (E) nên: 

Vậy elip (E) có phương trình chính tắc là:

II. ĐƯỜNG HYPEBOL

Bài 1: Viết phương trình hypebol sau đây dưới dạng chính tắc: 4x² – 9y² = 1

Giải nhanh:

III. ĐƯỜNG PARABOL

Bài 1: Viết phương trình các parabol sau đây dưới dạng chính tắc:

a. x =

b.

Giải nhanh:

a. với p =2

b. với p =

BAI TẬP CUỐI SGK

Bài tập 1: Phương trình nào sau đây là phương trình chính tắc của elip ?

a.

b.

c.

d.

Giải nhanh:

c.

Bài tập 2: Cho Elip (E) có phương trình chính tắc  . Tìm tọa độ các giao điểm của (E) với trục Ox, Oy và tọa độ các tiêu điểm của (E).

Giải nhanh:

Xét tọa độ giao điểm của (E) và trục Ox có:

Xét tọa độ giao điểm của (E) và trục Oy có: 

Ta có: a² = b² + c²

Bài tập 3: Viết phương trình chính tắc của elip (E), biết tọa độ hai giao điểm của (E) với Ox và Oy lần lượt là  A₁(-5; 0) và B₁(0;)

Giải nhanh:

(E) có phương trình chính tắc là: (a > b > 0)

Vì A₁(-5; 0) (E) nên

B₁(0;) (E) nên

Phương trình chính tắc của (E) là: :

Bài tập 4: Ta biết rằng Mặt Trăng chuyển động quanh Trái Đất theo quỹ đạo là một elip mà Trái Đất là một tiêu điểm. Elip có A1A₂=768 800km và B1B2=767 619 km (Nguồn: Ron Larson (2014), Precalculus Real Mathematics, Real People, Cengage (Hình 62). Viết phương trình chính tắc của elip đó.

Giải nhanh:

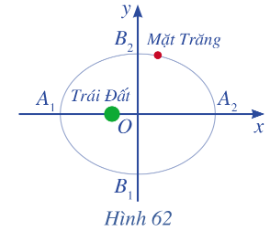
Ta có: A₁A₂ = 2a  = 768 800 a² = 384 400²

B₁B₂ = 2b = 767 619 b² = 383 809,5²

Phương trình chính tắc của Elip là: 

Bài tập 5: Những phương trình nào sau đây là phương trình chính tắc của Hypebol ?

a.

b.

c.

d.

Giải nhanh:

b.

c.

d.

Bài tập 6: Tìm tọa độ các tiêu điểm của đường hypebol trong mỗi trường hợp sau:

a.  

b.

Giải nhanh:

a. Toạ độ các tiêu điểm của Hypebol là: F₁(-5; 0) và F₂(5; 0)

b. Toạ độ các tiêu điểm của Hypebol là: F₁(- và F₂(

Bài tập 7: Viết phương trình chính tắc của Hypebol (H), biết N( nằm trên (H) và hoành độ một giao điểm của (H) đối với trục Ox bằng 3.

Giải nhanh:

Giả sử phương trình chính tắc của Hypebol có dạng:

(a > 0; b > 0)

Do hoành độ một giao điểm của (H) với trục Ox bằng 3.

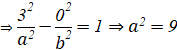
Do N( (H) nên: mà b² = 36. 

Vậy phương trình chính tắc của Hypebol là: (a > 0; b > 0)

Bài tập 8: Những phương trình nào sau đây là phương trình chính tắc của Parabol ?

a. y² = -2x

b. y² = 2x

c. x² = -2y

d. y² = x

Giải nhanh:

b. y² = 2x

d. y² = x

Bài tập 9: Tìm tọa độ tiêu điểm và viết phương trình đường chuẩn của đường parabol trong mỗi trường hợp sau:

a. y² =

b. y²  = 2x

Giải nhanh:

a. Tiêu điểm của parabol là: F và phương trình đường chuẩn là: x + = 0

b. Tiêu điểm của parabol là: F và phương trình đường chuẩn là: x + = 0 

Bài tập 10: Viết phương trình chính tắc của đường parabol, biết tiêu điểm là F(6;0).

Giải nhanh:

Giả sử phương trình chính tắc của parabol là: y² = 2px (p > 0)

Tiêu điểm F(6 ; 0) nên

Phương trình chính tắc của parabol là y² = 24x

Bài tập 11: Một chiếc đèn có mặt cắt ngang là hình parabol (Hình 63). Hình parabol có chiều rộng giữa hai mép vành là AB = 40 cm và chiều sâu h = 30 cm (h bằng khoảng cách từ O đến AB). Bóng đèn nằm ở tiêu điểm S. Viết phương trình chính tắc của parabol đó.

Giải nhanh:

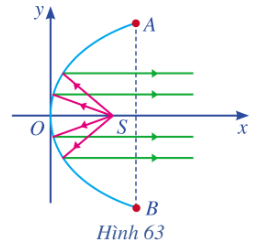
Phương trình chính tắc của parabol có dạng : y² = 2px (p > 0)

Vì AB = 40 nên khoảng cách từ A đến trục Ox là

h = khoảng cách từ O đến AB = khoảng cách từ A đến trục Oy = 30

Parabol đi qua điểm A(30; 20) => p =

Vậy phương trình chính tắc của Parabol là: y² = x