I. VỊ TRÍ TƯƠNG ĐỐI CỦA HAI ĐƯỜNG THẲNG

HĐ1:

Hai đường thẳng trong mặt phẳng thì cắt nhau hoặc song song hoặc trùng nhau. 

HĐ2:

Trong mặt phẳng toạ độ, cho hai đường thẳng $∆_1, ∆_2$ lần lượt có vectơ chỉ phương là $\overrightarrow{u_1}, \overrightarrow{u_2}$. Khi đó:

a. $∆_1$ cắt $∆_2$ khi và chỉ khi $\overrightarrow{u_1}, \overrightarrow{u_2}$ không cùng phương.

b. $∆_1$ song song với $∆_2$ khi và chỉ khi $\overrightarrow{u_1}, \overrightarrow{u_2}$ cùng phương và có một điểm thuộc một đường thẳng mà không thuộc đường thẳng còn lại.

c. $∆_1$ trùng với $∆_2$ khi và chỉ khi $\overrightarrow{u_1}, \overrightarrow{u_2}$ cùng phương và có một điểm thuộc cả hai đường thẳng đó. 

Kết luận: 

Trong mặt phẳng toạ độ, cho hai đường thẳng $∆_1$ và $∆_2$ lần lượt có vectơ chỉ phương là $\overrightarrow{u_1}, \overrightarrow{u_2}$. Khi đó

a. $∆_1$ cắt $∆_2$ khi và chỉ khi $\overrightarrow{u_1}, \overrightarrow{u_2}$ không cùng phương.

b. $∆_1$ song song với $∆_2$ khi và chỉ khi $\overrightarrow{u_1}, \overrightarrow{u_2}$ cùng phương và có một điểm thuộc một đường thẳng mà không thuộc đường thẳng còn lại.

c. $∆_1$ trùng với $∆_2$ khi và chỉ khi $\overrightarrow{u_1}, \overrightarrow{u_2}$ cùng phương và có một điểm thuộc cả hai đường thẳng đó. 

Chú ý:

+ $∆_1$ vuông góc với $∆_2$ khi và chỉ khi $\overrightarrow{u_1}, \overrightarrow{u_2}$ vuông góc với nhau.

+ Khi xét vị trí tương đối của hai đường thẳng, có thể dựa vào cặp vectơ pháp tuyến của hai đường thẳng đó. 

Ví dụ 1 (SGK – tr82)

Luyện tập 1:  

Ta có: $\overrightarrow{u_1}= (1; 1), \overrightarrow{u_2}= (2; 2)$. Ta thấy: $\overrightarrow{u_2}= 2\overrightarrow{u_1}$.

Chọn điểm $A(1; -2) \in ∆_1$. Thay toạ độ điểm $A$ vào phương trình đường thẳng $∆_2$ ta được: $t_2= \frac{1}{2} => A(1; -2) \in ∆_2$.

Vậy 2 đường thẳng $∆_1$ và $∆_2$ trùng nhau.

Nhận xét:

Cho hai đường thẳng $∆_1$ và $∆_2$ có phương trình lần lượt là:

$a_1x + b_1y + c_1$ và $a_2x + b_2y + c_2 = 0$

Xét hệ phương trình:

$\left\{\begin{matrix}
a_1x+b_1y+c_1= 0 & & \\
a_2x+b_2y+c_2= 0 & &
\end{matrix}\right.         (I)$

Khi đó

a. $∆_1$ cắt $∆_2$ khi và chỉ khi hệ $(I)$ có nghiệm duy nhất.

b. $∆_1$ song song với $∆_2$ khi và chỉ khi hệ $(I)$ vô nghiệm.

c. $∆_1$ trùng với $∆_2$ khi và chỉ khi hệ $(I)$ có vô số nghiệm. 

Ví dụ 2 (SGK – tr82)

Luyện tập 2:

+ Toạ độ giao điểm của đường thẳng d và ∆1 là nghiệm của hệ phương trình:

$\left\{\begin{matrix}
x+2y-2=0 & & \\
3x-2y+6=0 & &
\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix}
x=-1 & & \\
y= \frac{3}{2} & &
\end{matrix}\right.$

Vậy $d$ và $∆_1$ cắt nhau tại một điểm duy nhất.

+ Toạ độ giao điểm của đường thẳng $d$ và $∆_2$ là nghiệm của hệ phương trình:

$\left\{\begin{matrix}
x+2y-2=0 & & \\
x+2y+2=0 & &
\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix}
x+2y=2 & & \\
x+2y=-2 & &
\end{matrix}\right.$

Hệ phương trình vô nghiệm. 

Vậy $d$ và $∆_2$ song song với nhau. 

+ Toạ độ giao điểm của đường thẳng $d$ và $∆_3$ là nghiệm của hệ phương trình:

$\left\{\begin{matrix}
x+2y-2=0 & & \\
2x+4y-4=0 & &
\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix}
x+2y=2 & & \\
x+2y=2 & &
\end{matrix}\right.$

Hệ phương trình vô số nghiệm. 

Vậy $d$ và $∆_3$ trùng nhau.

II. GÓC GIỮA HAI ĐƯỜNG THẲNG

HĐ3:

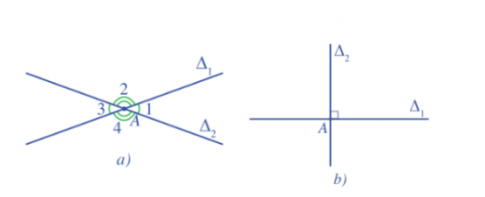
+ Trong hình 40a, ta có góc $\widehat{A_1}$ là một góc nhọn.

+ Trong hình 40b, ta có 4 góc tại đỉnh $A$ là góc vuông. 

Kết luận:

Hai đường thẳng $∆_1$ và $∆_2$ cắt nhau tạo thành bốn góc. 

+ Nếu hai đường thẳng $∆_1$ và $∆_2$ không vuông góc với nhau thì góc nhọn trong bốn góc tạo thành được gọi là góc giữa hai đường thẳng $∆_1$ và $∆_2$.

+ Nếu hai đường thẳng $∆_1$ và $∆_2$ vuông góc với nhau thì ta nói góc giữa hai đường thẳng $∆_1$ và $∆_2$ bằng $90^{\circ}$.

Góc giữa hai đường thẳng $∆_1$ và $∆_2$ được kí hiệu là $\widehat{\Delta_1,\Delta_2}$ hoặc $(∆_1, ∆_2)$

Quy ước: 

Khi $∆_1$ song song hoặc trùng với $∆_2$, ta nói góc giữa hai đường thẳng $∆_1$ và $∆_2$ bằng $0^{\circ}$.

Nhận xét:

Góc giữa hai đường thẳng luôn bé hơn hoặc bằng $90^{\circ}$, tức là $(∆_1, ∆_2) \leq 90^{\circ}$.

HĐ4:  

a. Độ lớn của góc giữa hai đường thẳng $∆_1, ∆_2$ và độ lớn của góc giữa hai vectơ $\overrightarrow{IA}, \overrightarrow{IB}$ có thể bằng nhau hoặc bù nhau. 

b.

+ Nếu $(\overrightarrow{IA}, \overrightarrow{IB}) \leq 90^{\circ}$ thì $(∆_1, ∆_2) = (\overrightarrow{IA}, \overrightarrow{IB})$. Do đó, $\cos (∆_1, ∆_2) = \cos (IA,IB) và cos(IA,IB) 0.

+ Nếu $(\overrightarrow{IA}, \overrightarrow{IB}) > 90^{\circ}$ thì $(∆_1, ∆_2) = 180^{\circ} - (\overrightarrow{IA}, \overrightarrow{IB})$. Do đó, $\cos (∆_1, ∆_2) = -\cos (\overrightarrow{IA}, \overrightarrow{IB})$ và $\cos (\overrightarrow{IA}, \overrightarrow{IB}) < 0$.

Từ hai trường hợp trên, ta suy ra $\cos (∆_1, ∆_2) = \left | \cos (\overrightarrow{IA}, \overrightarrow{IB}) \right |$

Nhận xét:

Do $(\overrightarrow{u_1}, \overrightarrow{u_2}) = (\overrightarrow{IA}, \overrightarrow{IB})$ nên $\cos (∆_1, ∆_2) = \left | \cos (\overrightarrow{u_1}, \overrightarrow{u_2}) \right |= \frac{\left | \overrightarrow{u_1}.\overrightarrow{u_2} \right |}{\left | \overrightarrow{u_1} \right |.\left | \overrightarrow{u_2} \right |}$

HĐ5:

Ta có: 

$\cos (\Delta_1,\Delta_2)= \left | \cos (\overrightarrow{u_1},\overrightarrow{u_2}) \right |= \frac{\left | a_1a_2+b_1b_2 \right |}{\sqrt{a_1^2+b_1^2}.\sqrt{a_2^2+b_2^2}}$

Kết luận:

Trong mặt phẳng toạ độ, cho hai đường thẳng $∆_1$ và $∆_2$ có vectơ chỉ phương lần lượt là $\overrightarrow{u_1}= (a_1; b_1), \overrightarrow{u_2}= (a_2; b_2)$.

Ta có: 

$\cos (\Delta_1,\Delta_2)= \frac{\left | a_1a_2+b_1b_2 \right |}{\sqrt{a_1^2+b_1^2}.\sqrt{a_2^2+b_2^2}}$

Nhận xét:

+ $∆_1 \perp ∆_2 ⟺ a_1a_2 + b_1b_2= 0$

+ Cho hai đường thẳng $\Delta_1$ và $∆_2$ có vectơ pháp tuyến lần lượt là $\overrightarrow{n_1}, \overrightarrow{n_2}$. Ta cũng có:

$\cos (∆_1, ∆_2) = \left | \cos (\overrightarrow{n_1},\overrightarrow{n_2}) \right |= \frac{\left | \overrightarrow{n_1}.\overrightarrow{n_2} \right |}{\left | \overrightarrow{n_1} \right |.\left | \overrightarrow{n_2} \right |}$

Ví dụ 3 (SGK – tr84)

Luyện tập 3:

a. Đường thẳng ∆1; ∆2 lần lượt có vectơ chỉ phương $\overrightarrow{u_1} = (3\sqrt3; 3); \overrightarrow{u_2}= (1; 0)$.

$\cos (∆_1, ∆_2)= = \frac{\left | 3\sqrt3.1+3.0 \right |}{(3\sqrt3)^2+3^2.\sqrt{1^2+0^2}}= \frac{3\sqrt3}{6}=\frac{\sqrt{3}}{2}$

Vậy $(∆_1, ∆_2)= 30^{\circ}$

b. Đường thẳng $∆_1; ∆_2$ lần lượt có vectơ pháp tuyến $\overrightarrow{n_1} = (2; -1); \overrightarrow{n_2}= (-1;3)$.

$\cos (\Delta_1, ∆_2)= \frac{\left | 2.(-1)+(-1).3 \right |}{\sqrt{2^2+(-1)^2}.\sqrt{(-1)^2+3^2}}= \frac{\sqrt2}{2}$

Vậy $(∆_1, ∆_2)= 45^{\circ}$.

III. KHOẢNG CÁCH TỪ MỘT ĐIỂM ĐẾN MỘT ĐƯỜNG THẲNG

HĐ6:

a. Do $MH$ vuông góc với đường thẳng $∆$ nên ta có vectơ chỉ phương của $MH$ là: $\overrightarrow{u}= (2; 1)$

b. Phương trình tham số của đường thẳng $MH$ đi qua $M(-1; 1)$ có vectơ chỉ phương $\overrightarrow{u}= (2; 1)$ là: 

$\left\{\begin{matrix}
x=-1+2t & & \\
y=1+t & &
\end{matrix}\right.\Leftrightarrow x-2y+3=0$

c. $H$ là giao điểm của $MH$ và đường thẳng $∆$.

Xét hệ phương trình: 

$\left\{\begin{matrix}
x-2y+3=0 & & \\
2x+y-4=0 & &
\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix}
x=1 & & \\
y=2 & &
\end{matrix}\right.$

Vậy toạ độ điểm $H$ là: $H(1; 2)$.

Độ dài đoạn thẳng $MH$ là: $MH = \sqrt{(1+1)^2+(2-1)^2}= \sqrt5$

Kết luận:

Trong mặt phẳng toạ độ $Oxy$, cho đường thẳng $∆$ có phương trình $ax + by + c = 0 (a^2 + b^2 > 0)$ và điểm $M(x_0; y_0)$. Khoảng cách từ điểm $M$ đến đường thẳng $∆$, kí hiệu là $d(M, ∆)$, được tính bởi công thức sau: 

$d(M, ∆)= \frac{\left | ax_o+by_o+c \right |}{\sqrt{a^2+b^2}}$

Chú ý: 

Nếu $M \in ∆$ thì $d(M, ∆) = 0$

Ví dụ 4 (SGK – tr 85)

Luyện tập 4:

a. Ta có: 

$∆: \frac{x}{-4}+ \frac{y}{2}= 1 ⟺ x - 2y + 4= 0$

Vậy khoảng cách từ $O$ đến $∆$ là: 

$D(O; ∆) = \frac{\left | 1.0-2.0+4 \right |}{\sqrt{1^2+2^2}} = \frac{4\sqrt5}{5}$

b. Lấy $M(0; 1) \in ∆_1$

$⇒ d(∆_1, ∆_2= d(M, ∆_2)= \frac{\left | 0-1-1 \right |}{\sqrt{1^2+(-1)^2}} = \sqrt2$