I. TỌA ĐỘ CỦA MỘT ĐIỂM

HĐ1:

a. Tung độ của điểm $A$ là: $2$.

Hoành độ của điểm $A$ là: $2$. 

b. Để xác định toạ độ của một điểm $M$ tuỳ ý trong mặt phẳng toạ độ $Oxy$, ta làm như sau:

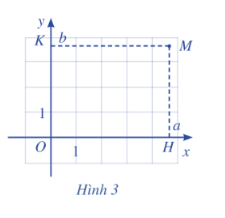
+ Từ $M$ kẻ đường thẳng vuông góc với trục hoành và cắt trục hoành tại điểm $H$ ứng với số $a$. Số $a$ là hoành độ của điểm $M$.

+ Từ $M$ kẻ đường thẳng vuông góc với trục tung và cắt trục tung tại điểm $K$ ứng với số $b$. Số $b$ là tung độ của điểm $M$. 

Cặp số $(a ; b)$ là toạ độ của điểm $M$ trong mặt phẳng toạ độ $Oxy$. Ta kí hiệu là $M (a ; b)$.

II. TỌA ĐỘ CỦA MỘT VECTƠ

HĐ2:

a. Ta có vectơ $\overrightarrow{OM}$ với điểm đầu là $O$ và điểm cuối là $M$ như Hình 4:

b. Cách xác định toạ độ của điểm $M$:

+ Từ $M$ kẻ đường thẳng vuông góc với trục hoành và cắt trục hoành tại điểm $H$ ứng với số $a$. Số $a$ là hoành độ của điểm $M$.

+ Từ $M$ kẻ đường thẳng vuông góc với trục tung và cắt trục tung tại điểm $K$ ứng với số $b$. Số $b$ là tung độ của điểm $M$. 

Cặp số $(a ; b)$ là toạ độ của điểm $M$ trong mặt phẳng toạ độ $Oxy$. Ta kí hiệu là $M (a ; b)$. 

Kết luận: 

Toạ độ của điểm $M$ được gọi là toạ độ của vectơ $\overrightarrow{OM}$.

Chú ý: Trong mặt phẳng toạ độ $Oxy$, ta có: 

+ $\overrightarrow{OM} = (a; b) \Leftrightarrow M (a ; b)$.

+ Vectơ $i$ có điểm gốc là $O$ và có toạ độ $(1 ; 0)$ gọi là vectơ đơn vị trên trục $Ox$. 

+ Vectơ $j$ có điểm gốc là $O$ và có toạ độ $(0; 1)$ gọi là vectơ đơn vị trên trục $Oy$ (Hình 5).

Ví dụ 1 (SGK – tr61)

HĐ3:

Để xác định điểm $A$, ta làm như sau:

+ Qua $O$ kẻ đường thẳng $d$ song song với giá của vectơ $\overrightarrow{u}$.

+ Lấy điểm $A$ trên đường thẳng $d$ sao cho hai vectơ $\overrightarrow{OA}, \overrightarrow{u}$ cùng hướng và độ dài đoạn thẳng $OA$ bằng độ dài vectơ $\overrightarrow{u}$.

Nhận xét: 

Với mỗi vectơ $\overrightarrow{u}$, ta xác định được duy nhất một điểm $A$ sao cho $\overrightarrow{OA} = \overrightarrow{u}$.

Kết luận: 

Với mỗi vectơ $\overrightarrow{u}$ trong mặt phẳng tọa độ $Oxy$, toạ độ của vectơ $\overrightarrow{u}$ là toạ độ của điểm $A$, trong đó $A$ là điểm sao cho $\overrightarrow{OA} = \overrightarrow{u}$.

Ví dụ 2 (SGK – tr62)

Luyện tập 1:

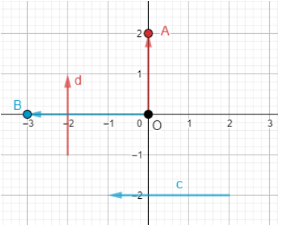
+ Ta vẽ vectơ $\overrightarrow{OA}= \overrightarrow{d}$ và $A(0; 2)$. Toạ độ $\overrightarrow{OA}$ chính là toạ độ của điểm $A$ nên $\overrightarrow{d}= (2; 2)$. 

+ Ta vẽ vectơ $\overrightarrow{OB}= \overrightarrow{c}$ và $A (-3; 0)$. Toạ độ $\overrightarrow{OB}$ chính là toạ độ của điểm $B$ nên $\overrightarrow{c}= (- 3; 0)$. 

HĐ4: 

a. Ta có: $\overrightarrow{OA}= \overrightarrow{u}$, mà $(a; b)$ là toạ độ của vectơ $\overrightarrow{u}$ nên điểm $A$ có hoành độ là $a$ và tung độ là $b$. 

b. Điểm $H$ biểu diễn số $a$ trên trục $Ox$ nên $\overrightarrow{OH}= \overrightarrow{ai}$.

c. Điểm $K$ biểu diễn số $b$ trên trục $Oy$ nên $\overrightarrow{OK}= \overrightarrow{bj}$.

d. Áp dụng quy tắc hình bình hành ta có: $\overrightarrow{OA}= \overrightarrow{OK} + \overrightarrow{OH}$.

Mà $\overrightarrow{OH} = \overrightarrow{ai}, \overrightarrow{OK} = \overrightarrow{bj}$ nên $\overrightarrow{u}= \overrightarrow{OA}= \overrightarrow{ai}+ \overrightarrow{bj}$ (đpcm).

Kết luận:

Trong mặt phẳng toạ độ $Oxy$, nếu $\overrightarrow{u}= (a; b)$ thì $\overrightarrow{u}= \overrightarrow{ai}+ \overrightarrow{bj}$ thì $\overrightarrow{u}= (a ; b)$. 

Chú ý:

Với $\overrightarrow{a}= (x_1 + y_1)$ và $\overrightarrow{b}= (x_2 + y_2)$, ta có: $\overrightarrow{a} = \overrightarrow{b} ⟺ \left\{\begin{matrix}x_1=x_2 &  & \\ y_1=y_2  &  &\end{matrix}\right.$

Như vậy, mỗi vectơ hoàn toàn được xác định khi biết toạ độ của nó. 

Ví dụ 3 (SGK – tr63).

Luyện tập 2: 

a. Vì $\overrightarrow{v}= (0; -7)$ nên $\overrightarrow{v}= 0\overrightarrow{i}+ (-7)\overrightarrow{j}= (-7)\overrightarrow{j}$.

b. Vì $B$ có toạ độ là $(- 1; 0)$ nên $\overrightarrow{OB}= (-1 ;0)$. Do đó: $\overrightarrow{OB}= (-1)\overrightarrow{i} + 0\overrightarrow{j}= -\overrightarrow{i}$.

III. LIÊN HỆ GIỮA TỌA ĐỘ CỦA ĐIỂM VÀ TỌA ĐỘ CỦA VECTƠ

HĐ5:

a. Từ hình vẽ ta có: $x_A= 2, y_A= 2$ và $x_B= 4, y_B= 3$.

b. Để xác định điểm $M$, ta làm như sau:

+ Từ điểm $O$, kẻ đường thẳng $d$ song song với giá của vectơ $\overrightarrow{AB}$.

+ Lấy điểm $M$ trên đường thẳng $d$ sao cho hai vectơ $\overrightarrow{AB}, \overrightarrow{OM}$ cùng hướng và độ dài đoạn thẳng $OM$ bằng độ dài vectơ $\overrightarrow{AB}$.

Điểm $M$ thoả mãn $\overrightarrow{OM}= \overrightarrow{AB}$ như hình vẽ. 

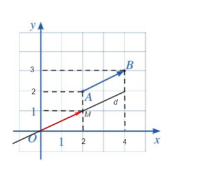
Ta có: hoành độ của điểm $M$ là $x_M = 2$; tung độ của điểm $M$ là $y_M = 1$. 

Toạ độ của điểm $M$ chính là toạ độ của vectơ $\overrightarrow{OM}$ nên $\overrightarrow{AB} = \overrightarrow{OM}= (2;1)$.

Vậy $a = 2; b = 1$. 

c. Ta có: $x_B - x_A = 4 - 2 = 2, y_B - y_A = 3 - 2 = 1$.

Vậy $x_B - x_A = a$ và $y_B - y_A = b$.

Nhận xét: 

Trong mặt phẳng toạ độ $Oxy$, cho hai điểm $A(x_A; y_A)$ và $B(x_B; y_B)$. Ta có: $\overrightarrow{AB}= (x_B - x_A; y_B - y_A)$.

Ví dụ 4

Luyện tập 3: 

Ta có:

$\overrightarrow{AB}= (5 - 1; -1 - 3)= (-4; 4)$

$\overrightarrow{DC}= (-2 - 2; 2-(-2))= (-4; 4)$

Vậy $\overrightarrow{AB}= \overrightarrow{DC}= (-4; 4)$

Ví dụ 5 (SGK – tr 64).