CHƯƠNG IX. PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG

BÀI 1. TỌA ĐỘ CỦA VECTƠ

1. TỌA ĐỘ CỦA VECTƠ ĐỐI VỚI MỘT HỆ TRỤC TỌA ĐỘ

HĐKP1:

+ Vectơ $\underset{i}{\rightarrow}$ có:

• độ lớn bằng 1

• phương: nằm ngang

• chiều: cùng chiều với chiều dương trục hoành

+ Vectơ $\underset{j}{\rightarrow}$ có:

• độ dài bằng 1

• phương: thẳng đứng

• chiều: cùng chiều với chiều dương trục tung

=> Độ lớn của $\underset{i}{\rightarrow}$ bằng độ lớn của $\underset{j}{\rightarrow}$, phương và chiều của hai vectơ vuông góc với nhau.

Kết luận:

• Trục tọa độ

Trục tọa độ (trục) là một đường thẳng trên đó đã xác định một điểm O (điểm gốc) và một vectơ $\underset{e}{\rightarrow}$ có độ dài bằng 1 gọi là vectơ đơn vị của trục.

Ta kí hiệu trục đó là (O; $\underset{e}{\rightarrow}$).

• Hệ trục tọa độ:

Hệ trục tọa độ (O; $\underset{i}{\rightarrow}$; $\underset{j}{\rightarrow}$) gồm hai trục (O; $\underset{i}{\rightarrow}$) và (O;$\underset{j}{\rightarrow}$) vuông góc với nhau. Điểm gốc O chung của hai trục gọi là gốc tọa độ. Trục (O;$\underset{i}{\rightarrow}$) được gọi là trục hoành và kí hiệu Ox, trục (O; $\underset{j}{\rightarrow}$) được gọi là trục tung và kí hiệu Oy. Các vectơ $\underset{i}{\rightarrow}$ và $\underset{j}{\rightarrow}$ là các vectơ đơn vị trên Ox và Oy. Hệ trục tọa độ (O; $\underset{i}{\rightarrow}$; $\underset{j}{\rightarrow}$) còn được kí hiệu là Oxy.

* Chú ý:

Mặt phẳng mà trên đó đã cho một hệ trục tọa độ Oxy được gọi là mặt phẳng tọa độ Oxy, hay gọi tắt là mặt phẳng Oxy.

• Tọa độ của một vectơ

HĐKP2:

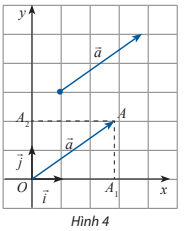
$\underset{a}{\rightarrow}$=$\underset{OA}{\rightarrow}$=$\underset{OA_{1}}{\rightarrow}$+$\underset{OA_{2}}{\rightarrow}$=x$\underset{i}{\rightarrow}$+y$\underset{j}{\rightarrow}$

Trong mặt phẳng Oxy, cặp số (x; y) trong biểu diễn $\underset{a}{\rightarrow}$ = x.$\underset{i}{\rightarrow}$ + y.$\underset{j}{\rightarrow}$ được gọi là tọa độ của vectơ $\underset{a}{\rightarrow}$, kí hiệu $\underset{a}{\rightarrow}$ = (x; y), x gọi là hoành độ, y gọi là tung độ của vectơ $\underset{a}{\rightarrow}$.

* Chú ý:

• $\underset{a}{\rightarrow}$ = (x; y) <=> $\underset{a}{\rightarrow}$ = x. $\underset{i}{\rightarrow}$ + y.$\underset{j}{\rightarrow}$

• Nếu cho $\underset{a}{\rightarrow}$ = (x; y) và b = (x'; y') thì

$\underset{a}{\rightarrow}$ = $\underset{b}{\rightarrow}$ <=> $\left\{\begin{matrix}x=x' & \\ y=y' & \end{matrix}\right.$

• Tọa độ của một điểm

HĐKP3:

$\underset{OM}{\rightarrow}$ = {x;y}

=> Trong mặt phẳng tọa độ, cho một điểm M tùy ý. Tọa độ vectơ $\underset{OM}{\rightarrow}$ được gọi là tọa độ của điểm M.

Nhận xét:

• Nếu $\underset{OM}{\rightarrow}$=(x;y) thì cặp số (x;y) là tọa độ của điểm M, kí hiệu M(x; y), x gọi là hoành độ, y gọi là tung độ của điểm M.

• M (x;y) <=> $\bar{OM}$=x$\underset{i}{\rightarrow}$+y$\underset{j}{\rightarrow}$

Chú ý: Hoành độ của điểm M còn được kí hiệu là x$_{M}$ ; tung độ của điểm M còn được kí hiệu là y$_{M}$. Khi đó ta viết M(x$_{M}$; y$_{M}$).

Ví dụ 1: SGK – tr 39

Thực hành 1.

a)

b) Do D(-1; 4), E(0; -3), F(5; 0) nên $\underset{OD}{\rightarrow}$ = (-1; 4), $\underset{OE}{\rightarrow}$ = (0; -3), $\underset{OF}{\rightarrow}$ = (5; 0)

c) $\underset{i}{\rightarrow}$ = (1; 0), $\underset{j}{\rightarrow}$ = (0; 1)

Vận dụng 1.

a) AB = DC = AC.cos 30$^{\circ}$ = 240.cos30$^{\circ}$ = 120$\sqrt{3}$ (km)

BC = AD = AC.sin30$^{\circ}$ = 240.sin30$^{\circ}$ = 120 (km)

b) $\underset{v}{\rightarrow}$ = 120$\sqrt{3} \underset{i}{\rightarrow}$ + 120$\underset{j}{\rightarrow}$

c) $\underset{v}{\rightarrow}$ = (120$\sqrt{3}$; 120)

2. BIỂU THỨC TỌA ĐỘ CỦA CÁC PHÉP TOÁN VECTƠ

HĐKP4:

a) $\underset{a}{\rightarrow}$ + $\underset{b}{\rightarrow}$ = a$_{1} \underset{i}{\rightarrow}$ + a$_{2} \underset{j}{\rightarrow}$ + b$_{1} \underset{i}{\rightarrow}$ + b$_{2} \underset{j}{\rightarrow}$ = (a$_{1}$1 + b$_{1}$)$\underset{i}{\rightarrow}$ + (a$_{2}$ + b$_{2}$)$\underset{j}{\rightarrow}$ 

$\underset{a}{\rightarrow}$ - $\underset{b}{\rightarrow}$ = a$_{1} \underset{i}{\rightarrow}$ + a$_{2}$j - b$_{1} \underset{i}{\rightarrow}$ - b$_{2} \underset{j}{\rightarrow}$ = (a$_{1}$ - b$_{1}$)$\underset{i}{\rightarrow}$ + (a$_{2}$ - b$_{2}$)$\underset{j}{\rightarrow}$

k$\underset{a}{\rightarrow}$ = k(a$_{1} \underset{i}{\rightarrow}$ + a$_{2} \underset{j}{\rightarrow}$) = ka$_{1} \underset{i}{\rightarrow}$ + ka$_{2} \underset{j}{\rightarrow}$

b) $\underset{a}{\rightarrow}$ . $\underset{b}{\rightarrow}$ = (a$_{1} \underset{i}{\rightarrow}$ + a$_{2} \underset{j}{\rightarrow}$)(b$_{1} \underset{i}{\rightarrow}$ + b$_{2} \underset{j}{\rightarrow}$) = a$_{1} \underset{i}{\rightarrow}$. b$_{1} \underset{i}{\rightarrow}$ +a$_{1} \underset{i}{\rightarrow}$. b$_{2} \underset{j}{\rightarrow}$ + a$_{2}$j. b$_{1} \underset{i}{\rightarrow}$ + a$_{2}$j. b$_{2} \underset{j}{\rightarrow}$

= a$_{1}$b$_{1} \underset{i}{\rightarrow}^{2}$+ a$_{1}$b$_{2} \underset{i}{\rightarrow}$$\underset{j}{\rightarrow}$ + a$_{2}$.b$_{1} \underset{i}{\rightarrow} \underset{j}{\rightarrow}$ + a$_{2}$b$_{2} \underset{j}{\rightarrow}^{2}$

= a$_{1}$b$_{1}$.1$^{2}$ + a$_{1}$b$_{2}$.0+ a$_{2}$.b$_{1}$.0 + a$_{2}$b$_{2}$.1$^{2}$ (vì $\underset{i}{\rightarrow} \perp  \underset{j}{\rightarrow}$)

= a$_{1}$b$_{1}$ + a$_{2}$b$_{2}$

⇒ Kết luận:

Cho hai vectơ $\underset{a}{\rightarrow}$=(a$_{1}$; a$_{2}$), $\underset{b}{\rightarrow}$=(b$_{1}$; b$_{2}$) và số thực k. Khi đó:

1) $\underset{a}{\rightarrow}$ + $\underset{b}{\rightarrow}$ = (a$_{1}$ + b$_{1}$ ; a$_{2}$ + b$_{2}$);

2) $\underset{a}{\rightarrow}$ - $\underset{b}{\rightarrow}$ = (a$_{1}$ - b$_{1}$ ; a$_{2}$ + b$_{2}$);

3) k.$\underset{a}{\rightarrow}$ = (k.a$_{1}$ ; ka$_{2}$);

4) $\underset{a}{\rightarrow}$ . $\underset{b}{\rightarrow}$ = a$_{1}$ .b$_{1}$ + a$_{2}$ .b$_{2}$);

Ví dụ 2: SGK-tr41

Thực hành 2:

a) $\underset{m}{\rightarrow}$ + $\underset{n}{\rightarrow}$ = (-6 + 0; 1 - 2) = (-6; -1)

$\underset{m}{\rightarrow}$ - $\underset{n}{\rightarrow}$ = (-6 - 0; 1 + 2) = (-6; 3)

10m = (10. (-6); 10. 1) = (-60; 10)

-4$\underset{n}{\rightarrow}$ = (-4. 0; -4.(-2)) = (0; 8)

b) $\underset{m}{\rightarrow}$ . $\underset{n}{\rightarrow}$ = -6. 0 + 1. (-2) = -2

(10$\underset{m}{\rightarrow}$).(-4$\underset{n}{\rightarrow}$) = -60. 0 + 10. 8 = 80

 Vận dụng 2:

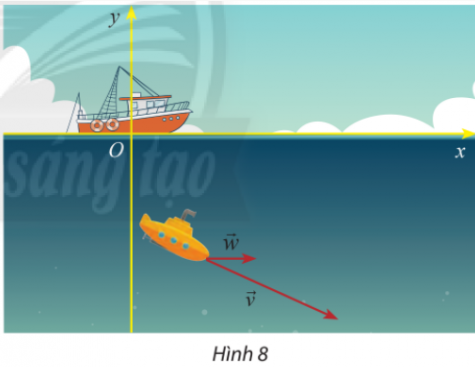
$\underset{v}{\rightarrow}$ + $\underset{w}{\rightarrow}$ = (10 +3,5; -8 + 0) = (13,5; -8)

3. ÁP DỤNG CỦA TỌA ĐỘ VECTƠ

Liên hệ giữa tọa độ của điểm và tọa độ của vectơ trong mặt phẳng

HĐKP5:

Vì A(x$_{A}$; y$_{A}$), B(x$_{B}$; y$_{B}$) 

=> $\underset{OA}{\rightarrow}$ = {x$_{A}$; y$_{A}$); $\underset{OB}{\rightarrow}$ = (x$_{B}$; y$_{B}$)

Ta có: $\underset{AB}{\rightarrow}$ = $\underset{OB}{\rightarrow}$ - $\underset{OA}{\rightarrow}$ = (x$_{B}$ - x$_{A}$; y$_{B}$ - y$_{A}$)

Kết luận:

Cho hai điểm A (x$_{A}$; y$_{A}$); B(x$_{B}$; y$_{B}$). Ta có:

$\underset{AB}{\rightarrow}$ = (x$_{B}$ – x$_{A}$ ; y$_{B}$ – y$_{A}$)

Ví dụ 3: SGK-tr42

Thực hành 3: E (9; 9) ; F(8; -7); G(0;-6)

$\underset{FE}{\rightarrow}$ = (x$_{E}$ - x$_{F}$; y$_{E}$ - y$_{F}$) = (9 - 8; 9 - (-7)) = (1; 16)

$\underset{FG}{\rightarrow}$ = (x$_{G}$ - x$_{F}$; y$_{G}$ - y$_{F}$) = (0 - 8; -6 -(-7)) = (-8; 1)

$\underset{EG}{\rightarrow}$ = (x$_{G}$ - x$_{E}$; y$_{G}$ - y$_{E}$) = (0 - 9; -6 - 9) = (-9; -15)

Tọa độ trung điểm của đoạn thẳng và trọng tâm của tam giác.

HĐKP6.

a) Vì M là trung điểm AB nên: $\underset{AM}{\rightarrow}$ = $\frac{1}{2} \underset{AB}{\rightarrow}$

$\underset{OM}{\rightarrow}$ - $\underset{OA}{\rightarrow}$ = $\frac{1}{2}$ ($\underset{OB}{\rightarrow}$ - $\underset{OA}{\rightarrow}$) 

$\underset{OM}{\rightarrow}$ = $\frac{1}{2}$ ($\underset{OA}{\rightarrow}$ + $\underset{OB}{\rightarrow}$)

b) Vì G là trọng tâm tam giác ABC nên 3$\underset{OG}{\rightarrow}$ = $\underset{OA}{\rightarrow}$ + $\underset{OB}{\rightarrow}$ + $\underset{OC}{\rightarrow}$

<=> $\underset{OG}{\rightarrow}$ = $\frac{1}{3}$ ($\underset{OA}{\rightarrow}$ + $\underset{OB}{\rightarrow}$ + $\underset{OC}{\rightarrow}$)

c) M($\frac{x_{A}+x_{B}}{2}$;$\frac{y_{A}+y_{B}}{2}$); G($\frac{x_{A}+x_{B}+x_{C}}{3}$;$\frac{y_{A}+y_{B}+y_{C}}{3}$)

Kết luận:

Cho hai điểm A (x$_{A}$; y$_{A}$) và B (x$_{B}$; y$_{B}$). Tọa độ trung điểm M (x$_{M}$; y$_{M}$) của đoạn thẳng AB là:

x$_{M}$ = $\frac{x_{A}+x_{B}}{2}$ ;  y$_{M}$ = $\frac{y_{A}+y_{B}}{2}$

Cho tam giác ABC có A (x$_{A}$; y$_{A}$); B(x$_{B}$ ; y$_{B}$); C (x$_{C}$; y$_{C}$). Tọa độ trọng tâm G (x$_{G}$; y$_{G}$) của tam giác ABC là:

x$_{G}$ =$\frac{x_{A}+x_{B}+x_{C}}{3}$;  y$_{G}$ = $\frac{y_{A}+y_{B}+y_{C}}{3}$;

Ví dụ 4: SGK-tr42

Thực hành 4.

a) Ta có: x$_{M}$ = $\frac{x_{Q}+x_{S}}{2}$ = $\frac{7+5}{2}$ = 6; y$_{M}$ = $\frac{y_{Q}+y_{S}}{2}$ = $\frac{-2+8}{2}$ = 3

Vậy M(6; 3)

b) Ta có: x$_{G}$ = $\frac{x_{Q}+x_{R}+x_{S}}{3}$=$\frac{7+(-4)+5}{3}$ =$\frac{8}{3}$; y$_{G}$ = $\frac{y_{Q}+y_{R}+y_{S}}{3}$; =$\frac{-2+9+8}{3}$ = 5

Vậy G($\frac{8}{3}$; 5)

Ứng dụng biểu thức tọa độ của các phép toán vectơ

HĐKP7.

a) $\underset{a}{\rightarrow} \perp  \underset{b}{\rightarrow}$ <=> $\underset{a}{\rightarrow}$. $\underset{b}{\rightarrow}$= 0 <=> a$_{1}$b$_{1}$ + a$_{2}$b$_{2}$ = 0

b) $\underset{a}{\rightarrow}$ và $\underset{b}{\rightarrow}$ cùng phương

<=> $\left\{\begin{matrix}a_{1}=tb_{1} & \\ a_{2}=tb_{2} & \end{matrix}\right.$ hay $\left\{\begin{matrix}b_{1}=ka_{1} & \\ b_{2}=ka_{2} & \end{matrix}\right.$  

<=> a$_{1}$b$_{1}$ + a$_{2}$b$_{2}$ = 0

c) |$\underset{a}{\rightarrow}$| = $\sqrt{(\underset{a}{\rightarrow})^{2}}$=$\sqrt{a_{1}^{2}+a_{2}^{2}}$;

d) $\underset{AB}{\rightarrow}$ = (x$_{B}$ - x$_{A}$; y$_{B}$ - y$_{A}$) 

=>AB = $\sqrt{(\underset{AB}{\rightarrow})^{2}}$=$\sqrt{(x_{B}-x_{A})^{2}+(y_{B}-y_{A})^{2}}$;

e) cos($\underset{a}{\rightarrow}$, $\underset{b}{\rightarrow}$) = $\frac{\underset{a}{\rightarrow}.\underset{b}{\rightarrow}}{|\underset{a}{\rightarrow}|.|\underset{b}{\rightarrow}|}$=$\frac{a_{1}b_{1}+a_{2}b_{2}}{\sqrt{a_{1}^{1}+a_{2}^{2}}.\sqrt{b_{1}^{2}+b_{2}^{2}}}$ ($\underset{a}{\rightarrow}$, $\underset{b}{\rightarrow}$ khác $\underset{0}{\rightarrow}$).

Kết luận:

Cho hai vectơ $\underset{a}{\rightarrow}$= (x$_{A}$; x$_{B}$), $\underset{b}{\rightarrow}$ = (y$_{A}$; y$_{B}$) và hai điểm A(x$_{A}$; y$_{A}$), B(x$_{B}$; y$_{B}$). Ta có:

• $\underset{a}{\rightarrow} \perp  \underset{b}{\rightarrow}$ <=> $\underset{a}{\rightarrow}$. $\underset{b}{\rightarrow}$= 0 <=> a$_{1}$b$_{1}$ + a$_{2}$b$_{2}$ = 0;

• $\underset{a}{\rightarrow}$ và $\underset{b}{\rightarrow}$ cùng phương <=>a$_{1}$b$_{1}$+a$_{2}$b$_{2}$=0;

•  |$\underset{a}{\rightarrow}$| = $\sqrt{(\underset{a}{\rightarrow})^{2}}$=$\sqrt{a_{1}^{2}+a_{2}^{2}}$ ;

• AB = $\sqrt{(x_{B}-x_{A})^{2}+(y_{B}-y_{A})^{2}}$

• cos($\underset{a}{\rightarrow}$, $\underset{b}{\rightarrow}$) = $\frac{\underset{a}{\rightarrow}.\underset{b}{\rightarrow}}{|\underset{a}{\rightarrow}|.|\underset{b}{\rightarrow}|}$=$\frac{a_{1}b_{1}+a_{2}b_{2}}{\sqrt{a_{1}^{1}+a_{2}^{2}}.\sqrt{b_{1}^{2}+b_{2}^{2}}}$($\underset{a}{\rightarrow}$, $\underset{b}{\rightarrow}$ khác $\underset{0}{\rightarrow}$)

Ví dụ 5: SGK-tr43

Thực hành 5.

a) Xét điểm H(x; y), ta có: $\underset{DH}{\rightarrow}$ = (x - 2; y - 2), $\underset{EH}{\rightarrow}$ = (x - 6; y - 2), $\underset{EF}{\rightarrow}$ = (-4; 4)

H(x; y) là chân đường cao của tam giác DEF kẻ từ D, nên ta có:

• $\underset{DH}{\rightarrow}$. $\underset{EF}{\rightarrow}$ (x - 2).(-4) + (y - 2). 4 = 0 => -4x + 4y = 0 (1)

• Hai vectơ $\underset{EH}{\rightarrow}$, $\underset{EF}{\rightarrow}$ cùng phương  (x - 6). 4 - (y - 2). (-4) = 0 => 4x + 4y - 32 = 0 (2)

Từ (1) và (2) ta có hệ phương trình:

$\left\{\begin{matrix}-4x+4y=0 & \\ 4x+4y-32=0 & \end{matrix}\right.$   

<=> $\left\{\begin{matrix}x=4 & \\ y=4 & \end{matrix}\right.$

Vậy H(4; 4)

b) Ta có: $\underset{DE}{\rightarrow}$ = (4; 0); $\underset{DF}{\rightarrow}$ = (0; 4); $\underset{EF}{\rightarrow}$ = (-4; 4)

DE = |$\underset{DE}{\rightarrow}$| = $\sqrt{4^{2}+0^{2}}$ = 4

DF = |$\underset{DF}{\rightarrow}$| = $\sqrt{0^{2}+4^{2}}$ = 4

EF = |$\underset{EF}{\rightarrow}$| = $\sqrt{(-4)^{2}+4^{2}}$ = 4$\sqrt{2}$

cosD = cos($\underset{DE}{\rightarrow}$, $\underset{DF}{\rightarrow}$) =$\frac{\underset{DE}{\rightarrow}.\underset{DF}{\rightarrow}}{DE.DF}$ = $\frac{4.0+0.4}{4.4}$ = 0  => $\widehat{D}$ = 90°

Nhận thấy tam giác DEF vuông cân tại D =>$\widehat{E}$ = $\widehat{F}$ = 45°

Vận dụng 3:

a) Ta có: $\underset{AB}{\rightarrow}$ = (60; 10), $\underset{AC}{\rightarrow}$ = (42; -43), $\underset{BC}{\rightarrow}$ = (-18; -53)

Suy ra: AB = |$\underset{AB}{\rightarrow}$| = $\sqrt{60^{2}+10^{2}}$ = 10$\sqrt{37} \approx $60,8

            AC = |$\underset{AB}{\rightarrow}$| = $\sqrt{42^{2}+(-43)^{2}} \approx $60,1

           cos$\widehat{BAC}$ = cos($\underset{AB}{\rightarrow}$, $\underset{AC}{\rightarrow}$)= $\frac{\underset{AB}{\rightarrow}.\underset{AC}{\rightarrow}}{AB.AC}$ = $\frac{60.42+10.(-43)}{60,8.60,1} \approx $ 0,57 => $\widehat{BAC}$  55°7'

b) Khoảng cách từ con tàu đến hòn đảo B là: AB $\approx $ 60,8 (km)

    Khoảng cách từ con tàu đến hòn đảo C là AC $\approx $ 60,1 (km)