Hoạt động 1: Vẽ elip bằng phần mềm GeoGebra

A. Vẽ elip theo phương trình chính tắc $\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1$

Thực hành 1: Vẽ các elip sau:

a. $\frac{x^{2}}{10} + \frac{y^{2}}{4} = 1$;

b. $\frac{x^{2}}{12} + \frac{y^{2}}{3} = 1$;

c. $\frac{x^{2}}{100} + \frac{y^{2}}{36} = 1$

Hướng dẫn giải:

a.

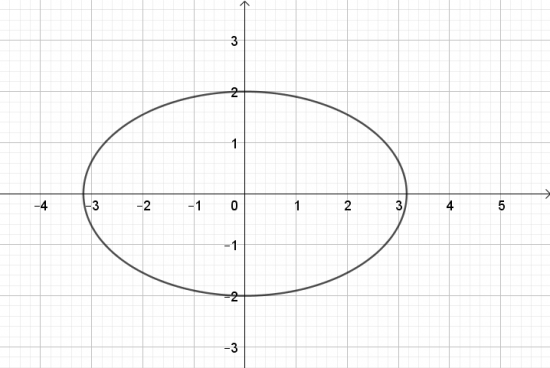
b.

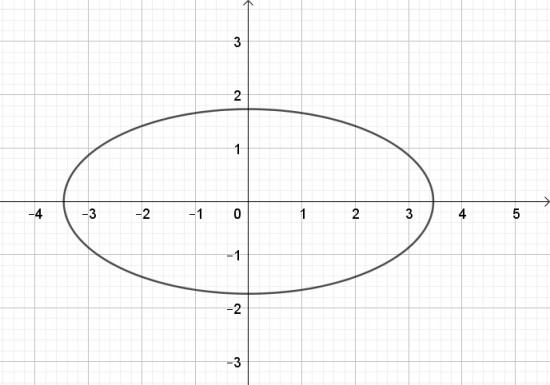
c.

B. Ứng dụng của elip trong thiết kế

Thực hành 2: Thiết kế một đường hầm có mặt cắt hình nửa elip cao 4 m, rộng 10 m.

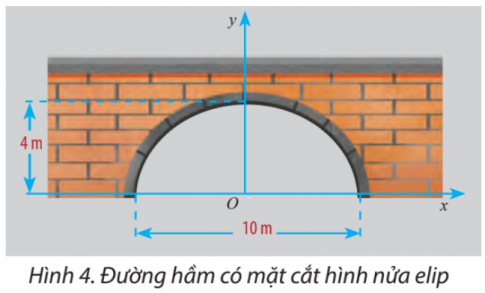
Hướng dẫn giải:

Ta có: b = 4, 2a = 10 $\Rightarrow$ a = 5.

Vậy phương trình chính tắc của elip (E) là: $\frac{x^{2}}{25} + \frac{y^{2}}{16} = 1$

Hoạt động 2: Vẽ hypebol bằng phần mềm GeoGebra

A. Vẽ hypebol theo phương trình chính tắc $\frac{x^{2}}{a^{2}} - \frac{y^{2}}{b^{2}} = 1$

Thực hành 3: Vẽ các hypebol sau:

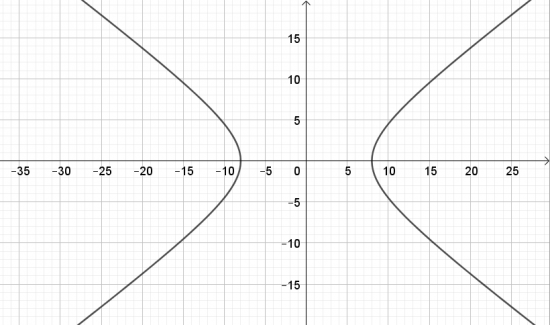
a. $\frac{x^{2}}{10} - \frac{y^{2}}{6} = 1$;

b. $\frac{x^{2}}{4} - \frac{yy^{2}}{3} = 1$;

c. $\frac{x^{2}}{64} - \frac{y^{2}}{36} = 1$.

Hướng dẫn giải:

a.

b.

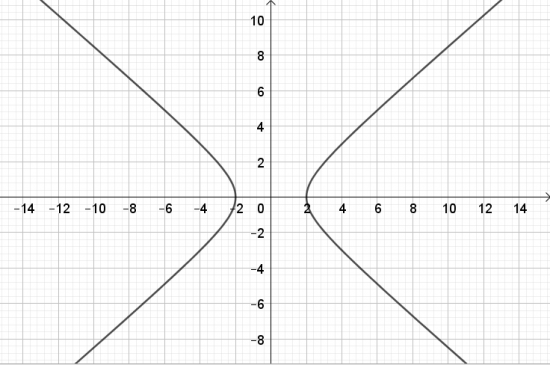
c.

Hoạt động 3: Vẽ parabol bằng phần mềm GeoGebra

A. Vẽ parabol theo phương trình chính tắc $y^{2} = 2px$

Thực hành 4: Vẽ các parabol sau:

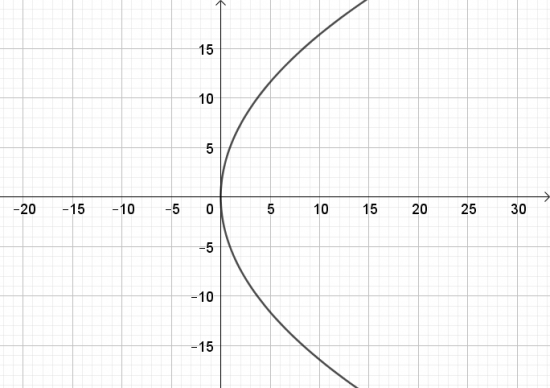
a. $y^{2} = 16x$;

b. $y^{2} = x$;

c. $y^{2} = 32x$.

Hướng dẫn giải:

a.

b.

c.

B. Ứng dụng của parabol trong thiết kế

Thực hành 5: Thiết kế một chóa đèn có mặt cắt hình parabol với kích thước được cho trong hình sau:

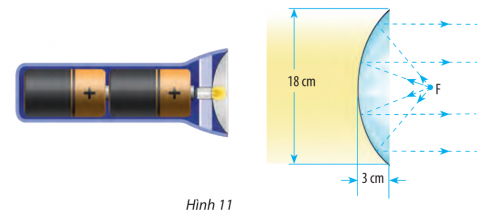
Hướng dẫn giải:

Gọi phương trình của parabol (P) là: $y^{2} = 2px$

Thay x = 3, y = 9 vào phương trình (P), ta được: $9^{2}$ = 2p. 3 $\Rightarrow$ p = $\frac{27}{2}$

$\Rightarrow$ (P): $y^{2} = 27x$