Trắc nghiệm Toán 8 chân trời sáng tạo bài 5 Hình chữ nhật - Hình vuông
Bài trắc nghiệm có đáp án. Câu hỏi và bài tập trắc nghiệm Toán 8 Bài 5 Hình chữ nhật - Hình vuông - sách chân trời sáng tạo. Học sinh luyện tập bằng cách chọn đáp án của mình trong từng câu hỏi. Dưới cùng của bài trắc nghiệm, có phần xem kết quả để biết bài làm của mình. Kéo xuống dưới để bắt đầu.
Câu 1: Hãy chọn câu sai. Hình chữ nhật có
- A. Bốn góc
- B. Hai đường chéo giao nhau tại trung điểm mỗi đường
C. Hai đường chéo vuông góc với nhau
- D. Các cạnh đối bằng nhau
Câu 2: Hình vuông là tứ giác có
- A. Có bốn cạnh bằng nhau
B. Có bốn góc bằng nhau
C. Có 4 góc vuông và bốn cạnh bằng nhau
- D. Cả A, B, C đều sai
Câu 3: Hãy chọn câu sai.
A. Hình thang có một góc vuông là hình chữ nhật
- B. Hình bình hành có một góc vuông là hình chữ nhật
- C. Hình bình hành có hai đường chéo bằng nhau là hình chữ nhật
- D. Hình thang cân có một góc vuông là hình chữ nhật
Câu 4: Khẳng định nào sau đây là sai?
- A. Hình vuông vừa là hình thoi vừa là hình chữ nhật
B. Hình vuông là hình chữ nhật nhưng không là hình thoi
- C. Hình vuông có hai đường chéo bằng nhau và vuông góc với nhau
- D. Hình vuông có đường chéo là phân giác các góc trong hình vuông
Câu 5: Nếu ABCD là hình vuông thì:
- A. AC = BD
- B. AC, BD giao nhau tại trung điểm mỗi đường
- C. AC ⊥ BD
D. Cả A, B, C đều đúng
Câu 6: Hãy chọn câu sai. Cho ABCD là hình chữ nhật có O là giao điểm hai đường chéo. Khi đó
- A. AC = BD
- B. AB = CD; AD = BC
- C. AO = OB
D. OC > OD
Câu 7: Chọn câu đúng: Cho tứ giác ABCD có:
- A.
thì tứ giác ABCD là hình chữ nhật
- B. AB = CD; AC = BD thì tứ giác ABCD là hình chữ nhật
C. AB = BC; AD // BC, Â = 900 thì tứ giác ABCD là hình chữ nhật
- D. AB // CD; AB = CD thì tứ giác ABCD là hình chữ nhật
Câu 8: Chọn câu sai. Tứ giác nào có hai đường chéo bằng nhau.
- A. Hình vuông
- B. Hình thang cân
- C. Hình chữ nhật
D. Hình thoi
Câu 9: Chọn câu trả lời đúng. Tứ giác nào có hai đường chéo vuông góc với nhau?
- A. Hình thoi
- B. Hình vuông
- C. Hình chữ nhật
D. Cả A và B
Câu 10: Cho tam giác ABC, đường cao AH. Gọi I là trung điểm của AC, E là điểm đối xứng với H qua I. Tứ giác AECH là hình gì?
A. Hình chữ nhật
- B. Hình bình hành
- C. Hình thang cân
- D. Hình thang vuông
Câu 11: Cho hình vuông ABCD. Trên các cạnh AB, BC, CD, DA lần lượt lấy các điểm E, F, G, H sao cho AE = BF = CG = DH sao cho AE = BF = CG = DH. Tứ giác EFGH là hình gì?
- A. Hình chữ nhật
B. Hình vuông
- C. Hình bình hành
- D. Hình thoi
Câu 12: Độ dài đường trung tuyến ứng với cạnh huyền của tam giác vuông có các cạnh góc vuông bằng 5cm, 12cm là:
A. 6,5cm
- B. 6cm
- C. 13cm
- D. 10cm
Câu 13: Cho hình thoi ABCD, O là giao điểm của hai đường chéo. Các tia phân giác 4 góc đỉnh O cắt các cạnh AB, BC, CD, DA theo thứ tự ở E, F, G, H. Tứ giác EFGH là hình gì?
- A. Hình chữ nhật
- B. Hình thoi
- C. Hình bình hành
D. Hình vuông
Câu 14: Cho tam giác ABC với ba trung tuyến AI, BD, CE đồng quy tại G. M và N lần lượt là trung điểm của GC và GB. Tứ giác MNED là hình gì?
- A. Hình chữ nhật
B. Hình bình hành
- C. Hình thang cân
- D. Hình thang vuông
Câu 15: Cho hình vuông có chu vi 28 cm. Độ dài cạnh hình vuông là:
- A. 4cm
B. 7 cm
- C. 14 cm
- D. 8 cm
Câu 16: Cho tam giác ABC vuông tại A, AC = 8cm, điểm M thuộc cạnh BC. Gọi D, E theo thứ tự là các chân đường vuông góc kẻ từ M đến AB, AC. Chu vi của tứ giác ADME bằng:
A. 16cm
- B. 38cm
- C. 18cm
- D. 12cm
Câu 17: Cho hình vuông có chu vi 16 cm. Bình phương độ dài một đường chéo của hình vuông là:
A. 32
- B. 16
- C. 24
- D. 18
Câu 18: Cho tứ giác ABCD, lấy M, N, P, Q lần lượt là trung điểm của các cạnh AB, BC, CD, DA. Tứ giác ABCD cần có điều kiện gì để MNPQ là hình chữ nhật
- A. AB = BC
- B. BC = CD
- C. AD = CD
D. AC⊥ BD
Câu 19: Cho hình bình hành ABCD có AB = a, BC = b (a > b). Các phân giác trong của góc A, B, C, D tạo thành tứ giác MNPQ. Tính độ dài đường chéo của hình chữ nhật MNPQ theo a, b.
- A. QN = a – 2b
B. QN = a – b
- C. QN = a + b
- D. QN =
Câu 20: Cho tứ giác ABCD. Gọi E, F, G, H theo thứ tự là trung điểm của AB, BC, CD, DA. Tìm điều kiện của tứ giác ABCD để hình bình hành EFGH là hình vuông.
A. BD ⊥ AC; BD = AC
- B. BD ⊥ AC
- C. BD = AC
- D. AC = BD và AB // CD
Câu 21: Cho hình chữ nhật ABCD có AB = a;AD = b. Cho M, N, P, Q là các đỉnh của tứ giác MNPQ và lần lượt thuộc các cạnh AB, BC, CD, DA. Tìm giá trị nhỏ nhất của chu vi tứ giác MNPQ.
- A. $a^{2}+b^{2}$
- B. $\sqrt{a^{2}+b^{2}}$
C. $2\sqrt{a^{2}+b^{2}}$
- D. $2(a^{2}+b^{2})$
Câu 22: Cho hình vuông ABCD. M là điểm nằm trong hình vuông. Gọi E, F lần lượt là hình chiếu của M trên cạnh AB và AD. Tứ giác AEMF là hình vuông khi.
A. M trên đường chéo AC
- B. M thuộc cạnh DC
- C. M thuộc đường chéo BD
- D. M tùy ý nằm trong hình vuông ABCD
Câu 23: Cho hình vuông có chu vi 20 cm. Bình phương độ dài một đường chéo của hình vuông là:
- A. 32
B. 50
- C. 25
- D. 30
Câu 24: Cho hình thang cân ABCD, đáy nhỏ AB = 6, CD = 18, AD = 10. Gọi I, K, M, L lần lượt là trung điểm của các đoạn BC, CA, AD và BD. Tính độ dài các cạnh AB, AL, AK.
- A. $AB = 6; AL=5; AK=\sqrt{61}$
- B. $AB = 6; AL=\sqrt{52}; AK=4$
C. $AB = 6; AL=4; AK=\sqrt{52}$
- D. $AB = 4; AL=6; AK=\sqrt{52}$
Câu 25: Cho tam giác ABC vuông tại A, điểm M thuộc cạnh huyền BC. Gọi D, E lần lượt là chân đường vuông góc kẻ từ M đến AB, AC. Điểm M ở vị trí nào trên BC thì DE có độ dài nhỏ nhất?
A. M là hình chiếu của A trên BC
- B. M là trung điểm của BC
- C. M trùng với B
- D. Đáp án khác
- Câu 26: Cho hình cuông ABCD, điểm E thuộc cạnh CD. Tia phân giác của góc ABE cắt AD ở K. Chọn câu đúng.
A. AK + CE = BE
- B. AK + CE = 2BE
- C. AK + CE = ½BE
- D. AK + CE > BE
Câu 27: Cho hình vuông ABCD cạnh 8 cm. M, N, P, Q là trung điểm các cạnh AB, BC, CD, DA. Tính diện tích tứ giác MNPQ.
- A. $S_{MNPQ}= 28cm^{2}$
- B. $S_{MNPQ}= 30cm^{2}$
- C. $S_{MNPQ}= 16cm^{2}$
D. $S_{MNPQ}= 32cm^{2}$
Câu 28: Cho tam giác ABC cân tại A, đường trung tuyến AM. Gọi I là trung điểm của AC. K là điểm đối xứng với M qua điểm I. Tìm điều kiện của tam giác ABC để tứ giác AMCK là hình vuông
A. Tam giác ABC vuông cân tại A
- B. Tam giác ABC vuông cân tại B
- C. Tam giác ABC đều
- D. Tam giác ABC vuông cân tại C
Câu 29: Cho tam giác ABC vuông cân tại A. Trên cạnh BC lấy các điểm H, G sao cho BH = HG = GC. Qua H và G kẻ các đường vuông góc với BC, chúng cắt AB và AC theo thứ tự tại E và F. Cho BC = 9 cm. Tính chu vi của tứ giác EFGH.
A. 12 cm
- B. 9 cm
- C. 16 cm
- D. 20 cm
Câu 30: Cho tam giác ABC vuông tại A. Điểm M thuộc BC. Qua M dựng đường thẳng song song với AB cắt AC tại D. Qua M dựng đường thẳng song song với AC cắt AB tại E. Tìm vị trí điểm M để tứ giác ADME là hình vuông.
A. M là chân đường phân giác của  xuống cạnh BC.
- B. M là chân đường cao hạ từ đỉnh A xuống cạnh BC.
- C. M là chân đường trung tuyến từ đỉnh A xuống cạnh BC.
- D. Đáp án khác.

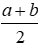
Bình luận