Câu 1: Hãy chọn câu sai

• A. Hai tam giác bằng nhau thì đồng dạng
• B. Hai tam giác đều luôn đồng dạng với nhau
• C. Hai tam giác đồng dạng là hai tam giác có tất cả các cặp góc tương ứng bằng nhau và các cặp cạnh tương ứng tỉ lệ

• D. Hai tam giác vuông luôn đồng dạng với nhau

Câu 2: Hãy chọn câu đúng.

• A. Hai tam giác bằng nhau thì đồng dạng

• B. Hai tam giác đồng dạng thì bằng nhau
• C. Hai tam giác bằng nhau thì không đồng dạng
• D. Hai tam giác vuông luôn đồng dạng với nhau

Câu 3: Nếu tam giác ABC có MN // BC (với M Є AB, N Є AC) thì

• A. ΔAMN đồng dạng với ΔACB
• B. ΔABC đồng dạng với MNA

• C. ΔAMN đồng dạng với ΔABC

• D. ΔABC đồng dạng với ΔANM

Câu 4: Cho tam giác ABC đồng dạng với tam giác A’B’C’. Hãy chọn phát biểu sai:

• A. $\widehat{A}=\widehat{A'}$
• B. $\frac{A'B'}{AB}=\frac{A'C'}{AC}$

• C. $\frac{A'B'}{AB}=\frac{BC}{B'C'}$

• D. $\widehat{B}=\widehat{B'}$

Câu 5: Cho tứ giác ABCD có đường chéo BD chia tứ giác đó thành hai tam giác đồng dạng ΔABD và ΔBDC. Chọn câu đúng nhất.

• A. AB // DC
• B. ABCD là hình thang
• C. ABCD là hình bình hành

• D. Cả A, B đều đúng

Câu 6: Cho tam giác ABC và hai điểm M, N lần lượt thuộc các cạnh BC, AC sao cho MN // AB. Chọn kết luận đúng.

• A. ΔAMN đồng dạng với ΔABC
• B. ΔABC đồng dạng với MNC

• C. ΔNMC đồng dạng với ΔABC

• D. ΔCAB đồng dạng với ΔCMN

Câu 7: Hình thang ABCD (AB // CD) có AB = 10cm, CD = 25cm, hai đường chéo cắt nhau tại O.

Chọn khẳng định đúng.

• A. ΔAOB ⁓ ΔCOD với tỉ số đồng dạng k = 2

• B. $\frac{AO}{OC}$=$\frac{2}{3}$

• C. ΔAOB ⁓ ΔCOD với tỉ số đồng dạng k = $\frac{2}{5}$

• D. ΔAOB ⁓ ΔCOD với tỉ số đồng dạng k = $\frac{5}{2}$

Câu 8: Cho tam giác ABC, điểm M thuộc cạnh BC sao cho 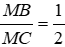. Đường thẳng đi qua M và song song với AC cắt AB ở D. Đường thẳng đi qua M và song song với AB cắt AC ở E. Tỉ số chu vi hai tam giác ΔDBM và ΔEMC là

• A. $\frac{1}{2}$

• B. $\frac{1}{3}$
• C. $\frac{2}{3}$
• D. $\frac{1}{4}$

Câu 9: Hãy chọn câu đúng. Tam giác ABC đồng dạng với tam giác MNP theo tỉ số $\frac{2}{3}$ biết chu vi của tam giác ABC bằng 40 cm. Chu vi của tam giác MNP là:

• A. 60 cm

• B. 20 cm
• C. 30 cm
• D. 45 cm

Câu 10: Hãy chọn câu trả lời đúng. Nếu tam giác ABC đồng dạng với tam giác A’B’C’ theo tỉ số k thì tỉ số chu vi của tam giác A’B’C’ và ABC bằng

• A. 1

• B. $\frac{1}{k}$

• C. k
• D. $k^{2}$

Câu 11: Hãy chọn câu đúng. Nếu tam giác ABC đồng dạng với tam giác MNP theo tỉ số k thì tam giác MNP đồng dạng với tam giác ABC theo tỉ số:

• A. $\frac{1}{k^{2}}$

• B. $\frac{1}{k}$

• C. k
• D. $k^{2}$

Câu 12: Cho hình bình hành ABCD. Trên đường chéo AC lấy điểm E sao cho AC = 3AE. Qua E vẽ đường thẳng song song với CD, cắt AD và BC theo thứ tự ở M và N. Cho các khẳng định sau

Số khẳng định đúng là:

• A. 1    
• B. 2

• C. 3

• D. 0

Câu 13: Cho  ΔABC nhọn, kẻ đường cao BD và CE, vẽ các đường cao DF và EG của ΔADE. ΔABD đồng dạng với tam giác nào dưới đây?

• A. ΔAEG

• B. ΔABC
• C. Cả A và B
• D. Không có tam giác nào

Câu 14: Cho tứ giác ABCD có đường chéo BD chia tứ giác đó thành hai tam giác đồng dạng ΔABD và ΔBDC. Tính các độ dài BD, BC biết AB = 2cm, AD = 3cm, CD = 8cm.

• A. BD = 5cm, BC = 6cm
• B. BD = 6cm, BC = 4cm
• C. BD = 6cm, BC = 6cm

• D. BD = 4cm, BC = 6cm

Câu 15: Hãy chọn câu đúng. Cho tam giác ABC có AB = AC = 5cm, BC = 4 cm đồng dạng với tam giác MNP theo tỉ số $\frac{2}{7}$. Chu vi của tam giác MNP là:

• A. 4 cm
• B. 21 cm
• C. 14 cm

• D. 49 cm

Câu 16: Cho tam giác ABC, điểm M thuộc cạnh BC sao cho 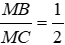. Đường thẳng đi qua M và song song với AC cắt AB ở D. Đường thẳng đi qua M và song song với AB cắt AC ở E. Biết chu vi tam giác ABC bằng 30cm. Chu vi của các tam giác DBM và EMC lần lượt là

• A. 10cm; 15cm
• B. 12cm; 16cm
• C. 20cm; 10cm

• D. 10cm; 20cm

Câu 17: Hãy chọn câu đúng. Nếu tam giác ABC đồng dạng với tam giác MNP theo tỉ số k = 2 thì tam giác MNP đồng dạng với tam giác ABC theo tỉ số:

• A. 2     
• B. 2    

• C.   

• D. 4

Câu 18: Cho ΔABC đồng dạng với ΔDEF và 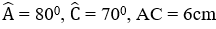. Số đo góc E là:

• A. 80°

• B. 30°

• C. 70°
• D. 50°

Câu 19: Cho ΔABC vuông tại A, đường cao AH. Gọi I và K lần lượt là hình chiếu của H lên AB và AC. Tam giác AIK đồng dạng với tam giác nào dưới đây? 

• A. ACB

• B. ABC
• C. CAB
• D. BAC

Câu 20: Cho tứ giác ABCD có đường chéo BD chia tứ giác đó thành hai tam giác đồng dạng ΔABD ⁓ ΔBDC.

Chọn câu sai.

• A. 
• B. ABCD là hình thang
• C. BD2 = AB.DC

• D. AD // BC

Câu 21: MNP đồng dạng ΔRKS theo tỉ số m. Ta có:

• A. MN = m.RK
• B. NP = m.KS
• C. MP = m.RS

• D. KS = m.NP

Câu 22: Cho hình bình hành ABCD. Trên đường chéo AC lấy điểm E sao cho AC = 3AE. Qua E vẽ đường thẳng song song với CD, cắt AD và BC theo thứ tự ở M và N. Cho các khẳng định sau

Chọn câu đúng.

• A. (I) đúng, (II) và (III) sai    
• B. (I) và (II) đúng, (III) sai

• C. Cả (I), (II), (III) đều đúng 

• D. Cả (I), (II), (III) đều sai

Câu 23: Chọn câu trả lời đúng: Có ΔHKI đồng dạng ΔEFG có HK = 5 cm, KI = 7 cm, HI = 8 cm, EF = 2,5 cm.Ta có:

• A. EG = 3,5 cm
• B. EG  = 16 cm

• C. EG = 4 cm

• D. EG = 14 cm

Câu 24: Cho hình thang vuông ABCD ($\widehat{A}=\widehat{D}=90^{\circ}$) có AB = 16 cm, CD = 25 cm, BD = 20 cm. Tam giác ABD đồng dạng với tam giác nào dưới đây?

• A. ΔBDC

• B. ΔCBD
• C. ΔBCD
• D. ΔDCB

Câu 26: Tỉ số các cạnh bé nhất của 2 tam giác đồng dạng bằng $\frac{2}{5}$. Tính chu vi p, p′ của 2 tam giác đó, biết p′ − p = 18?

• A. p = 12; p′ = 30

• B. p = 30; p′ = 12
• C. p = 30; p′ = 48
• D. p = 48; p′ = 30

Câu 27: Cho ΔABC có AB = 15 cm, AC = 20 cm, BC = 25 cm. Đường phân giác $\widehat{BAC}$ cắt BC tại D. Tỉ số diện tích của ΔABD và $\widehat{ACD}$ là?

• A.  $\frac{1}{4}$
• B.  $\frac{1}{2}$

• C.  $\frac{3}{4}$

• D.  $\frac{1}{3}$

Câu 28: ΔABC đồng dạng ΔDEF theo tỉ số k1, ΔMNP đồng dạng ΔDEF theo tỉ số k2. Vậy ΔABC ΔMNP theo tỉ số nào?

• A. k1
• B. $\frac{k2}{k1}$
• C. k1.k2

• D.  $\frac{k1}{k2}$

Câu 29: Cho hình bên, ABCD là hình thang (AB//CD) có AB = 12,5cm; CD = 28,5cm; 

$\widehat{DAB}$=$\widehat{DBC}$. Tính độ dài đoạn BD gần nhất bằng bao nhiêu?

• A. 17,5   
• B. 18
• C. 18,5   

• D. 19

Câu 30: Hãy chọn câu đúng. Hai ΔABC và ΔDEF có $\widehat{A}=80^{\circ}$, $\widehat{B}=70^{\circ}$, $\widehat{F}=30^{\circ}$ ,BC=6cm. Nếu ΔABC đồng dạng với ΔDEF thì:

• A. $\widehat{D}=170^{\circ}$; EF=6cm
• B. $\widehat{E}=80^{\circ}$; EF=6cm
• C. $\widehat{D}=70^{\circ}$

• D. $\widehat{C}=70^{\circ}$