Dễ hiểu giải Toán 11 Chân trời bài 2 Các quy tắc tính đạo hàm
Giải dễ hiểu Dễ hiểu giải Toán 11 Chân trời bài 2 Các quy tắc tính đạo hàm. Trình bày rất dễ hiểu, nên tiếp thu Toán 1 Chân trời dễ dàng. Học sinh nắm được kiến thức và biết suy rộng ra các bài tương tự. Thêm 1 dạng giải mới để mở rộng tư duy. Danh mục các bài giải trình bày phía dưới
Nếu chưa hiểu - hãy xem: => Lời giải chi tiết ở đây
CHƯƠNG VII: ĐẠO HÀM
BÀI 2. CÁC QUY TẮC ĐẠO HÀM
CÂU HỎI MỞ ĐẦU
Giả sử hàm số f(x) và g(x) lần lượt có đạo hàm tại x0 là f'(x0) và g'(x0). Làm thế nào để tính đạo hàm của các hàm số là tổng, hiệu, tích hoặc thương của f(x) và g(x) tại x0?
Giải nhanh:
Tìm giới hạn của tổng, hiệu, tích hoặc thương của f(x) và g(x) tại x0.
1. ĐẠO HÀM CỦA HÀM SỐ y = xn , n ∈ N*
Khám phá 1 trang 42 Toán 11 tập 2 Chân trời: a) Dùng định nghĩa tính đạo hàm của hàm số y = x tại điểm x = x0.
b) Nhắc lại đạo hàm của các hàm số y = x2; y = x3 đã tìm được ở bài học trước. Từ đó, dự đoán đạo hàm của hàm số y = xn với n ∈ℕ*
Giải nhanh:
a) ![]() .
.
b) ![]()
Dự đoán: ![]()
Thực hành 1 trang 43 Toán 11 tập 2 Chân trời: Tính đạo hàm của hàm số y = x10 tại x = −1 và x = ![]()
Giải nhanh:
![]()
![]()
2. ĐẠO HÀM CỦA HÀM SỐ Y=![]()
Khám phá 2 trang 43 Toán 11 tập 2 Chân trời: Dùng định nghĩa, tính đạo hàm của hàm số y = ![]() tại điểm x=x0 với x0>0
tại điểm x=x0 với x0>0
Giải nhanh:
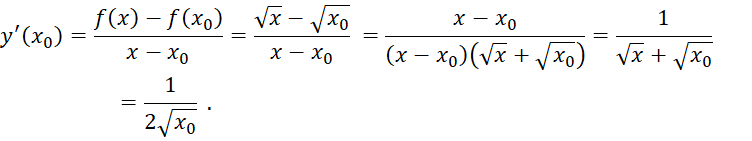
Thực hành 2 trang 43 Toán 11 tập 2 Chân trời: Viết phương trình tiếp tuyến của đồ thị hàm số y = ![]() tại điểm có hoành độ bằng 4
tại điểm có hoành độ bằng 4
Giải nhanh:
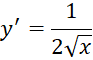
![]() .
.
Với ![]() thì
thì ![]() .
.
Phương trình tiếp tuyến của đồ thị tại điểm có hoành độ bằng 4 là:
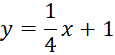
Thực hành 3 trang 43 Toán 11 tập 2 Chân trời: Tìm đạo hàm của các hàm số:
a) y= ![]() tại x = 1
tại x = 1
b) y = ![]() tại x = -
tại x = -![]()
Giải nhanh:
a) ![]()
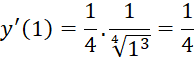
b) ![]()
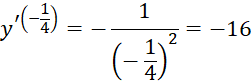
3. ĐẠO HÀM CỦA HÀM SỐ LƯỢNG GIÁC
Khám phá 3 trang 44 Toán 11 tập 2 Chân trời: Cho biết ![]() Dùng định nghĩa tính đạo hàm của hàm số y = sinx
Dùng định nghĩa tính đạo hàm của hàm số y = sinx
Giải nhanh:
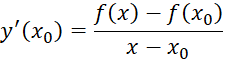
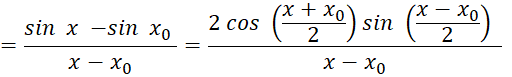
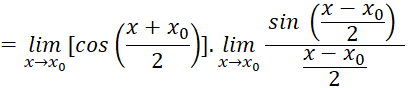
![]()
Thực hành 4 trang 44 Toán 11 tập 2 Chân trời: Tính đạo hàm của hàm số y = tanx tại x= ![]()
Giải nhanh:
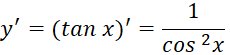
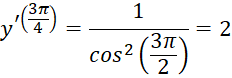
Khám phá 4 trang 44 Toán 11 tập 2 Chân trời: Cho biết ![]() 1 và
1 và ![]() 1. Dùng định nghĩa tính đạo hàm của các hàm số:
1. Dùng định nghĩa tính đạo hàm của các hàm số:
a) y = ex
b) y = lnx
Giải nhanh:
a) ![]()
b) ![]()
Thực hành 5 trang 44 Toán 11 tập 2 Chân trời: Tìm đạo hàm của các hàm số
a) y = 9x tại x = 1
b) y = lnx tại x = ![]()
Giải nhanh:
a) ![]()
![]()
b) ![]() .
.
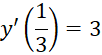
5. ĐẠO HÀM CỦA TỔNG, HIỆU, TÍCH, THƯƠNG CỦA HAI HÀM SỐ
Khám phá 5 trang 45 Toán 11 tập 2 Chân trời: Cho f(x) và g(x) là hai hàm số có đạo hàm tại x0. Xét hàm số h(x) = f(x) + g(x).
Ta có ![]() =
= ![]() nên
nên
h’(x) = ![]() =
= ![]() = ... +...
= ... +...
Chọn biểu thức thích hợp thay cho chỗ chấm để tìm h'(x0).
Giải nhanh:
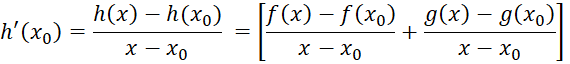
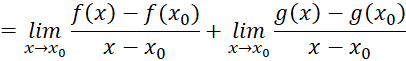
![]()
Thực hành 6 trang 46 Toán 11 tập 2 Chân trời: Tính đạo hàm của các hàm số sau:
a) y = xlog2x
b) y = x3ex
Giải nhanh:
a) ![]()
![]()
b) ![]()
6. ĐẠO HÀM CỦA HÀM HỢP
Khám phá 6 trang 46 Toán 11 tập 2 Chân trời: Cho hàm số u = sinx và hàm số y=u2
a) Tính y theo x
b) Tính y′x (đạo hàm của y theo biến x), y′u (đạo hàm của y theo biến u) và u′x (đạo hàm của u theo biến x) rồi so sánh y′x với y′u.u′x
Giải nhanh:
a) ![]() .
.
b) ![]()
![]()
![]()
![]()
![]()
Có ![]()
Vậy ![]() .
.
Thực hành 7 trang 47 Toán 11 tập 2 Chân trời: Tính đạo hàm của các hàm số sau:
a) y = (2x3+3)2
b) y = cos3x
c) y = log2 (x2+2)
Giải nhanh:
a) ![]() .
.
b) ![]() .
.
c) ![]()
7. ĐẠO HÀM CẤP 2
Khám phá 7 trang 47 Toán 11 tập 2 Chân trời: Một chuyển động thẳng xác định bởi phương trình s(t)=2t3+4t+1, trong đó s tính bằng mét và t là thời gian tính bằng giây
a) Tính vận tốc tức thời v(t) tại thời điểm t
b) Đạo hàm v'(t) biểu thị tốc độ thay đổi của vận tốc theo thời gian, còn gọi là gia tốc của chuyển động, kí hiệu a(t). Tính gia tốc của chuyển động tại thời điểm t = 2
Giải nhanh:
a) ![]() .
.
b) ![]()
![]() .
.
Thực hành 8 trang 48 Toán 11 tập 2 Chân trời: Tính đạo hàm cấp hai của các hàm số sau:
a) y = x2−x
b) y = cosx
Giải nhanh:
a) ![]() .
.
![]()
b) ![]() .
.
![]()
Vận dụng trang 49 Toán 11 tập 2 Chân trời: Một hòn sỏi rơi tự do có quãng đường rơi tính theo thời gian t là s(t) = 4,9t2, trong đó s tính bằng mét và t tính bằng giây. Tính gia tốc rơi của hòn sỏi lúc t = 3
Giải nhanh:
![]()
![]()
![]()
BÀI TẬP
Bài tập 1 trang 41 Toán 11 tập 2 Chân trời: Tính đạo hàm của các hàm số sau:
a) y = ![]()
b) y = ![]()
c) y = ![]()
d) ![]()
Giải nhanh:
a) ![]() .
.
b)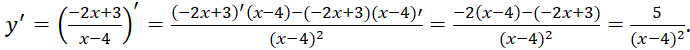
c) 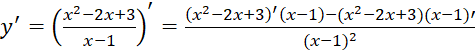
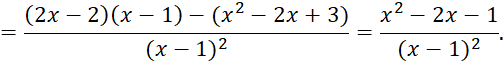
d) ![]()
Bài tập 2 trang 50 Toán 11 tập 2 Chân trời: Tính đạo hàm của các hàm số sau:
y = sin 3x
y =
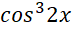
y =
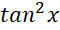
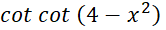
Giải nhanh:
a) ![]()
b) ![]()
c) ![]()
d) ![]()
Bài tập 3 trang 49 Toán 11 tập 2 Chân trời: Tính đạo hàm của các hàm số sau:
a) y = ![]()
b) y = ![]()
c) y = ![]()
Giải nhanh:
a) ![]()
![]()
b) ![]()
c) ![]() .
.
Bài tập 4 trang 49 Toán 11 tập 2 Chân trời: Tính đạo hàm cấp hai của các hàm số sau:
a) y = ![]()
b) y = xex
Giải nhanh:
a)![]()
![]()
b) ![]()
![]()
Bài tập 5 trang 49 Toán 11 tập 2 Chân trời: Cân nặng trung bình của một bé gái trong độ tuổi từ 0 đến 36 tháng có thể được tính gần đúng bởi hàm số ![]() , trong đó t được tính bằng tháng và w được tính bằng pound. Tính tốc độ thay đổi cân nặng của bé gái đó tại thời điểm 10 tháng tuổi
, trong đó t được tính bằng tháng và w được tính bằng pound. Tính tốc độ thay đổi cân nặng của bé gái đó tại thời điểm 10 tháng tuổi
Giải nhanh:
![]()
![]()
![]() (pound/tháng).
(pound/tháng).
Bài tập 6 trang 49 Toán 11 tập 2 Chân trời: Một công ty xác định rằng tổng chi phí của họ, tính theo nghin đô-la, để sản xuất x mặt hàng là C(x) = ![]() và công ty lên kế hoạch nâng sản lượng trong t tháng kể từ nay theo hàm số x(t) = 20t+40. Chi phí sẽ tăng nhanh thế nào sau 4 tháng kể từ khi công ty thực hiện kế hoạch đó?
và công ty lên kế hoạch nâng sản lượng trong t tháng kể từ nay theo hàm số x(t) = 20t+40. Chi phí sẽ tăng nhanh thế nào sau 4 tháng kể từ khi công ty thực hiện kế hoạch đó?
Giải nhanh:
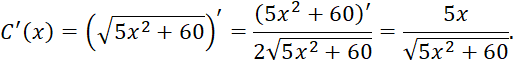
![]()
Khi đó , tốc độ tăng chi phí của công ty sau ![]() tháng là :
tháng là : ![]() .
.
Tốc độ tăng chi phí của công ty sau 4 tháng kể từ khi công ty thực hiện kế hoạch đó là :
![]() (nghìn đô – la/tháng).
(nghìn đô – la/tháng).
Bài tập 7 trang 49 Toán 11 tập 2 Chân trời: Trên Mặt trăng, quãng đường rơi tự do của một vật được cho bởi công thức s(t) = 0,81t2, trong đó t là thời gian được tính bằng giây và s tính bằng mét. Một vật được thả rơi từ độ cao 200m phía trên Mặt trăng. Tại thời điểm t = 2 sau khi thả vật đó, tính
a) Quãng đường vật đã rơi
b) Gia tốc của vật
Giải nhanh:
a) ![]()
b) Có ![]()
![]()
![]()
Nếu chưa hiểu - hãy xem: => Lời giải chi tiết ở đây
Nội dung quan tâm khác
Thêm kiến thức môn học
Giải bài tập những môn khác
Giải sgk lớp 11 KNTT
Giải sgk lớp 11 CTST
Giải sgk lớp 11 cánh diều
Giải SBT lớp 11 kết nối tri thức
Giải SBT lớp 11 chân trời sáng tạo
Giải SBT lớp 11 cánh diều
Giải chuyên đề học tập lớp 11 kết nối tri thức
Giải chuyên đề toán 11 kết nối tri thức
Giải chuyên đề ngữ văn 11 kết nối tri thức
Giải chuyên đề vật lí 11 kết nối tri thức
Giải chuyên đề hóa học 11 kết nối tri thức
Giải chuyên đề sinh học 11 kết nối tri thức
Giải chuyên đề kinh tế pháp luật 11 kết nối tri thức
Giải chuyên đề lịch sử 11 kết nối tri thức
Giải chuyên đề địa lí 11 kết nối tri thức
Giải chuyên đề mĩ thuật 11 kết nối tri thức
Giải chuyên đề âm nhạc 11 kết nối tri thức
Giải chuyên đề công nghệ chăn nuôi 11 kết nối tri thức
Giải chuyên đề công nghệ cơ khí 11 kết nối tri thức
Giải chuyên đề tin học 11 định hướng Khoa học máy tính kết nối tri thức
Giải chuyên đề tin học 11 định hướng Tin học ứng dụng kết nối tri thức
Giải chuyên đề quốc phòng an ninh 11 kết nối tri thức
Giải chuyên đề hoạt động trải nghiệm hướng nghiệp 11 kết nối tri thức
Giải chuyên đề học tập lớp 11 chân trời sáng tạo
Giải chuyên đề học tập lớp 11 cánh diều
Trắc nghiệm 11 Kết nối tri thức
Trắc nghiệm 11 Chân trời sáng tạo
Trắc nghiệm 11 Cánh diều
Bộ đề thi, đề kiểm tra lớp 11 kết nối tri thức
Đề thi Toán 11 Kết nối tri thức
Đề thi ngữ văn 11 Kết nối tri thức
Đề thi vật lí 11 Kết nối tri thức
Đề thi sinh học 11 Kết nối tri thức
Đề thi hóa học 11 Kết nối tri thức
Đề thi lịch sử 11 Kết nối tri thức
Đề thi địa lí 11 Kết nối tri thức
Đề thi kinh tế pháp luật 11 Kết nối tri thức
Đề thi công nghệ cơ khí 11 Kết nối tri thức
Đề thi công nghệ chăn nuôi 11 Kết nối tri thức
Đề thi tin học ứng dụng 11 Kết nối tri thức
Đề thi khoa học máy tính 11 Kết nối tri thức
Bộ đề thi, đề kiểm tra lớp 11 chân trời sáng tạo
Bộ đề thi, đề kiểm tra lớp 11 cánh diều
Đề thi Toán 11 Cánh diều
Đề thi ngữ văn 11 Cánh diều
Đề thi vật lí 11 Cánh diều
Đề thi sinh học 11 Cánh diều
Đề thi hóa học 11 Cánh diều
Đề thi lịch sử 11 Cánh diều
Đề thi địa lí 11 Cánh diều
Đề thi kinh tế pháp luật 11 Cánh diều
Đề thi công nghệ cơ khí 11 Cánh diều
Đề thi công nghệ chăn nuôi 11 Cánh diều
Đề thi tin học ứng dụng 11 Cánh diều
Đề thi khoa học máy tính 11 Cánh diều

Bình luận