CHƯƠNG VII: ĐẠO HÀM

BÀI 1. ĐẠO HÀM

CÂU HỎI MỞ ĐẦU

Giữa tốc độ của xe và quãng đường mà xe đi được có mối liên hệ như thế nào? Nếu biết quãng đường s(t) tại mọi thời điểm t thì có thể tính được tốc độ của xe tại mỗi thời điểm không?

Giải nhanh: 

Khi biết quãng đường s(t) tại mọi thời điểm t thì ta có thể tính được tốc độ của xe tại mỗi thời điểm

1. ĐẠO HÀM

Khám phá 1 trang 37 Toán 11 tập 2 Chân trời: Quãng đường rơi tự do của một vật được biểu diễn bởi công thức s(t) = 4,9t² với t là thời gian tính bằng giây và s tính bằng mét.

Vận tốc trung bình của chuyển động này trên khoảng thời gian [5; t] hoặc [t; 5] được tính bằng công thức 

a) Hoàn thiện bảng sau về vận tốc trung bình trong những khoảng thời gian khác nhau. Nêu nhận xét về khi t càng gần 5

b) Giới hạn lim_t→5được gọi là vận tốc tức thời của chuyển động tại thời điểm t₀ = 5. Tính giá trị này.

c) Tính giới hạn lim_t→to để xác định vận tốc tức thời của chuyển động tại thời điềm t₀ nào đó trong quá trình rơi của vật.

Giải nhanh:

Quãng đường rơi tự do của vật biểu diễn bởi công thức:

a) 

Khi càng gần thì giá trị của càng gần về .

b) Tại , ta có:

c)

Thực hành 1 trang 39 Toán 11 tập 2 Chân trời: Tính đạo hàm của hàm số f(x) = x³ 

Giải nhanh:

Với bất kì ta có:

Vận dụng trang 39 Toán 11 tập 2 Chân trời: Với tình huống trong Khám phá 1, hãy tính vận tốc tức thời của chuyển động lúc t = 2

Giải nhanh:

（）

2. Ý NGHĨA HÌNH HỌC CỦA ĐẠO HÀM 

Khám phá 2 trang 39 Toán 11 tập 2 Chân trời: Cho hàm số y = f(x) = x² có đồ thị (C) và điểm M(1;) thuộc (C)

a) Vẽ (C) và tính f'(1)

b) Vẽ đường thẳng d đi qua điểm M và có hệ số góc bằng f'(1). Nêu nhận xét về vị trí tương đối giữa d và (C) 

Giải nhanh:

a)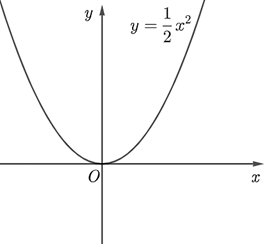

b) đi qa và có hệ số góc bằng nên:

Ta có hình vẽ sau:

Thực hành 2 trang 40 Toán 11 tập 2 Chân trời: Cho (C) là đồ thị của hàm số f(x) = và điểm M(1;1) ∈ (C). Tính hệ số góc của tiếp tuyến của (C) tại điểm M và viết phương trình tiếp tuyến đó

Giải nhanh:

Ta có:

Phương trình tiếp tuyến của tại điểm là:

.

3. SỐ e

Khám phá 3 trang 40 Toán 11 tập 2 Chân trời: Một người gửi tiết kiệm khoản tiền A triệu đồng (gọi là vốn) với lãi suất r/năm theo thể thức lãi kép (tiền lãi sau mỗi kì hạn được cộng gộp vào vốn). Tính tổng số tiền vốn và lãi sau một năm của người gửi nếu kì hạn là:

a) một năm

b) một tháng

Lưu ý: Nếu một năm được chia thành n kì hạn (n∈N*) thì lãi suất mỗi kì hạn là

Giải nhanh:

a) Nếu người gửi với kì hạn một năm số tiền lãi sau một năm là A.r.

Tổng số tiền vốn và lãi sau một năm của người gửi là:

b) Nếu người gửi với kì hạn một tháng thì số tiền lãi sau tháng thứ nhất là:

Tổng số tiền vốn và lãi sau tháng thứ nhất là: 

Số tiền lãi sau than thứ hai là:

Tổng số tiền vốn và lãi sau tháng thứ hai là:

Tổng số tiền vốn và lãi sau 1 năm là:

Tiền lãi và vốn tính theo kì hạn tương ứng là: ; 

; 

;...

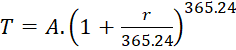Tổng quát, nếu một năm được chia thành kì hạn thì

(với .

Khi kì hạn càng ngắn thì càng lớn, do đói càng lớn. Người ta chứng minh được rằng có giới hạn hữu hạn

(với là số vô tỉ và

Khi kì hạn trở nên rất ngắn (m dần đến ) thì dần đến , và do đó dần đến

Thực hành 3 trang 41 Toán 11 tập 2 Chân trời: Một người gửi tiết kiệm khoản tiền 5 triệu đồng vào ngân hàng với lãi suất 6%/năm và theo thể thức lãi kép liên tục. Tính tổng số tiền vốn và lãi mà người đó nhận được sau:

a) 1 ngày

b) 30 ngày

Giải nhanh:

a) (đồng)

b) (đồng)

BÀI TẬP

Bài tập 1 trang 41 Toán 11 tập 2 Chân trời: Dùng định nghĩa để tính đạo hàm của các hàm số sau:

a) f(x) = −x²

b) f(x) = x³ − 2x

c) f(x)=

Giải nhanh:

a) Với bất kì ta có:

b) Với bất kì ta có :

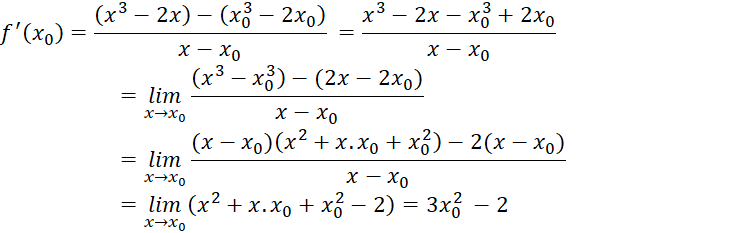
c) Với bất kì , ta có:

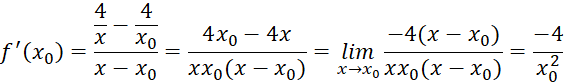
Bài tập 2 trang 41 Toán 11 tập 2 Chân trời: Cho hàm số f(x) = −2x² có đồ thị (C) và điểm A(1; −2) ∈ (C). Tính hệ số góc của tiếp tuyến với (C) tại điểm A.

Giải nhanh:

Hệ số góc của tiếp tuyến với tại điểm là :

Bài tập 3 trang 42 Toán 11 tập 2 Chân trời: Viết phương trình tiếp tuyến của đồ thị hàm số y=x3

a) Tại điểm (-1;1)

b) Tại điểm có hoành độ bằng 2

Giải nhanh: 

Với bất kì ta có:

a) Vì điểm không thuộc đồ thị hàm số nên không có phương trình tiếp tuyến tại điểm .

b) Với nên . Do đó .

Hệ số góc của tiếp tuyến tại là: .

Phương trình tiếp tuyến của tại điểm là :

hay .

Bài tập 4 trang 42 Toán 11 tập 2 Chân trời: Một chuyển động thẳng xác định bởi phương trình s(t)=4t³+6t+2, trong đó s tính bằng mét và t là thời gian tính bằng giây. Tính vận tốc tức thời của chuyển động tại t = 2

Giải nhanh:

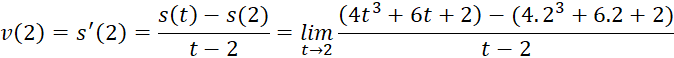
Bài tập 5 trang 42 Toán 11 tập 2 Chân trời: Một người gửi tiết kiệm khoản tiền 10 triệu đồng vào một ngân hàng với lãi suất 5%/năm. Tính tổng số tiền vốn và lãi mà người đó nhận được sau một năm, nếu tiền lãi được tính theo thể thức

a) lãi kép với kì hạn 6 tháng

b) lãi kép liên tục

Giải nhanh: 

a) (đồng).

b) (đồng).

Bài tập 6 trang 42 Toán 11 tập 2 Chân trời: Trên Mặt trăng, quãng đường rơi tự do của một vật được cho bởi công thức h(t) = 0,81t², với t được tính bằng giây và h tính bằng mét. Hãy tính vận tốc tức thời của vật được thả rơi tự do trên Mặt trăng tại thời điểm t = 2

Giải nhanh:

Vậy vận tốc tức thời của chuyển động lúc là