Giải câu 18 bài: Luyện tập 1 sgk Toán hình 7 tập 1 Trang 114
Câu 18: Trang 114 - Sgk toán 7 tập 1
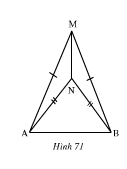
Xét bài toán: “ΔAMB và ΔANB có MA = MB, NA = NB (hình 71). Chứng minh rằng \(\widehat{AMN}=\widehat{BMN}\)."
1) Hãy ghi giả thiết và kết luận của bài toán
2) Hãy sắp xếp bốn câu sau đây một cách hợp lí để giải bài toán
a) Do đó Δ MNA = ΔBMN (c.c.c)
b) MN: cạnh chung
MA = MB (giả thiết)
NA = NB (giả thiết)
c) Suy ra \(\widehat{AMN}=\widehat{BMN}\)(2 góc tương ứng)
d)\(\Delta\)AMB và \(\Delta\)ANB có:
1) Dựa vào hình đề bài ra, ta có giả thiết của bài toán như sau:
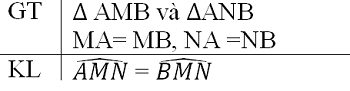
2) Các ý được sắp xếp hợp lí để chứng minh \(\widehat{AMN}=\widehat{BMN}\)
d)\(\Delta\)AMB và \(\Delta\)ANB có:
b) MN: cạnh chung
MA = MB (giả thiết)
NA = NB (giả thiết)
a) Do đó Δ MNA = ΔBMN (c.c.c)
c) Suy ra \(\widehat{AMN}=\widehat{BMN}\)(2 góc tương ứng)

Bình luận