BÀI 9: TÍNH CHẤT BA ĐƯỜNG PHÂN GIÁC CỦA TAM GIÁC

1. ĐƯỜNG PHÂN GIÁC CỦA TAM GIÁC

Bài 1: Vẽ và cắt hình tam giác ABC rồi gấp hình sao cho cạnh AB trùng với cạnh AC ta được nếp gấp AD (Hình 1). Đoạn thẳng AD nằm trên tia phân giác của góc nào trong tam giác ABC.

Giải rút gọn:

AD là tia phân giác của

Bài 2:Trong Hình 3, hãy vẽ các đường phân giác GM, EN và FP của tam giác EFG. 

Giải rút gọn:

2. TÍNH CHẤT BA ĐƯỜNG PHÂN GIÁC CỦA TAM GIÁC

Bài 1: Vẽ một tam giác trên giấy. Cắt rời tam giác ra khỏi tờ giấy rồi gấp hình tam giác đó để xác định ba đường phân giác của tam giác (Hình 4). Em hãy quan sát và nhận xét xem ba đường phân giác có cùng đi qua một điểm hay không ? 

Giải rút gọn:

3 đường phân giác đi qua một điểm.

Bài 2: Một nông trại nằm trên mảnh đất hình tam giác có ba cạnh tường rào tiếp giáp với ba con đường ( Hình 7). Hỏi phải đặt trạm quan sát ở đâu để nó cách đều ba cạnh tường rào? 

Giải rút gọn:

Trạm quan sát cách đều ba cạnh tường rào => vị trí trạm quan sát là giao của ba đường phân giác trong của tam giác tạo bởi 3 cạnh tường.

BÀI TẬP CUỐI SGK

Bài 1:Trong hình 8, I là giao điểm ba đường phân giác của tam giác ABC.

a) Cho biết IM = 6 ( Hình 8a). Tính IK và IN.

b) Cho biết IN = x + 3, IM = 2x -3 ( Hình 8b). Tìm x.

Giải rút gọn:

a) IK = IN = IM = 6

b) IN = IM ⬄ x + 3 = 2x – 3 ⬄ x = 6 

Bài 2: Cho tam giác ABC cân tại A. Kẻ đường trung tuyến AM. Tia phân giác của góc B cắt AM tại I. Chứng minh rằng CI là tia phân giác của góc C.

Giải rút gọn:

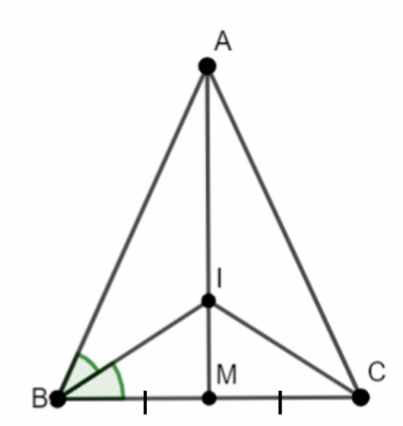
+) BM = CM, chung AM, AB = AC => ΔAMB = ΔAMC (c.c.c)

    => => AM là tia phân giác

+) ΔABC có 2 tia phân giác BI và AM cắt nhau tại I 

   => CI là tia phân giác

Bài 3: Cho tam giác ABC cân tại A. Tia phân giác của các góc B và C cắt nhau tại M. Tia AM cắt BC tại H. Chứng minh H là trung điểm của BC. 

Giải rút gọn: 

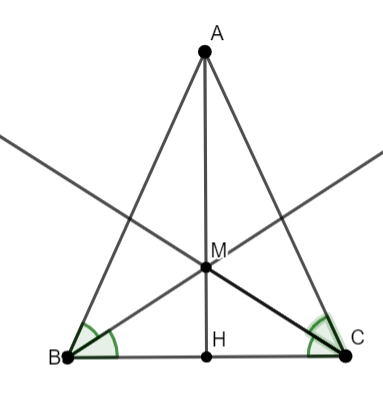
+) ΔABC có 2 tia phân giác BM và CM cắt nhau tại M

   => AM là tia phân giác =>

+) AB = AC, , chung AH => ∆AHB = ∆AHC (c.g.c)

   => BH = CH => H là trung điểm BC (đpcm)

Bài 4: Cho tam giác DEF. Tia phân giác của góc D và E cắt nhau tại I. Qua I kẻ đường thẳng song song với EF, đường thẳng này cắt DE tại M, cắt DF tại N. Chứng minh rằng ME + NF = MN.

Giải rút gọn:

+) EI là tia phân giác =>  =

+) MI // EF => = (so le trong)

=>  = => ∆MIE cân tại M => MI = ME

+) FI là tia phân giác => =

+) IN // EF => (so le trong)

=> = => ∆ INF cân tại N => IN = FN

+) Ta có ME + NF = MI + IN = MN

Bài 5: Cho tam giác ANM vuông tại A. Tia phân giác của góc M và N cắt nhau tại I. Tia MI cắt AN tại R. Kẻ RT vuông góc với AI tại T. Chứng minh rằng AT = RT. 

Giải rút gọn: 

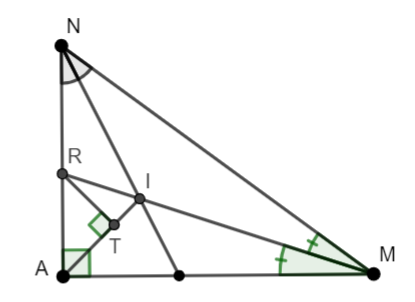
+) ∆NAM : 2 đường phân giác NI và MI cắt nhau tại I => AI là tia phân giác =>= = 90° : 2 = 45°

+) ∆TRA có = 90° - 45°= 45°

=> => ∆RAT vuông cân tại T => TR = TA

Bài 6: Ba thành phố A, B, C được nối với nhau bởi ba xa lộ ( Hình 9 ). Người ta muốn tìm một địa điểm để làm một sân bay sao cho địa điểm này phải cách đều ba xa lộ đó. Hãy xác định vị trí của sân bay thỏa mãn điều kiện trên và giải thích cách thực hiện.

Giải rút gọn:

Sân bay cách đều 3 cạnh ΔABC  => vị trí là giao 3 đường phân giác của ΔABC.