BÀI TẬP CUỐI CHƯƠNG 8

Bài 1: 

Cho tam giác ABC cân tại A... Hai đường cao BE và CF cắt nhau tại H.

a) Chứng minh rằng ∆ BEC = ∆ CFB.

b) Chứng minh rằng ∆ AHF = ∆ AHE.

c) Gọi I là trung điểm của BC. Chứng minh rằng ba điểm A, H, I thẳng hàng.

Giải rút gọn:

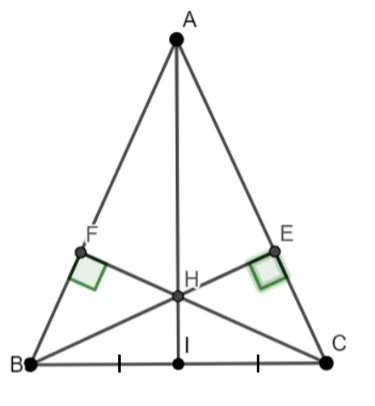
a) +) = , chung BC => ΔFBC = ΔECB ( cạnh huyền- góc nhọn)

b) +) ΔFBC = ΔECB => FB = EC

    +) AB = AC => AB – FB = AC – EC => AF = AE

    +) AF = AE , chung AH => ΔFAH = ΔEHA ( cạnh huyền – cạnh góc vuông)

c) +) ΔABC có 2 đường cao BE ∩ CF = H => H là trực tâm => AH ⊥ BC (1)

    +) BI = CI, AB = AC, chung AI => ΔAIB = ΔAIC (c.c.c)

    => = mà + = 180° => = = 90° => AI ⊥ BC (2)

   Từ (1) và (2) => A, I, H thẳng hàng.

Bài 2: Cho tam giác ABC vuông tại A, vẽ đường cao AH. Trên tia đối của tia HA lấy điểm M sao cho H là trung điểm của AM.

a) Chứng minh tam giác ABM cân.

b) Chứng minh rằng ∆ ABC = ∆ MBC.

Giải rút gọn:

a) AH = MH , chung HB => ∆ABH = ∆MBH (2 cạnh góc vuông)

    => AB = MB => ∆BAM cân tại B

b) ∆ABH = ∆MBH => =

    AB = MB , = , chung BC => ∆ABC = ∆MBC (c.g.c)

Bài 3: Cho tam giác ABC vuông tại A ( AB , AC), vẽ đường cao AH. Trên tia đối của HC lấy điểm D sao cho HD = DC.

a) Chứng minh AC = AD.

b) Chứng minh rằng…

Giải rút gọn:

a) HC = HD , chung AH => ∆HAC = ∆HAD (2 cạnh góc vuông) => AC = AD

b) +) ∆BHA vuông tại H => + = 90°

    +) ∆ABC vuông tại A  => +  = 90°

     => = (1)

+) AC = AD => ΔDAC cân tại A =>  = (2)

   Từ (1) và (2) => =

Bài 4: Cho tam giác vuông ABC vuông tại A (AB < AC). Trên cạnh BC lấy điểm N sao cho BA = BN. Kẻ BE ⊥ AN (E thuộc AN).

a) Chứng minh rằng BE là tia phân giác của góc ABN.

b) Kẻ đường cao AH của tam giác ABC. Gọi K là giao điểm của AH với BE. Chứng minh rằng NK // CA.

c) Đường thẳng BK cắt AC tại F. Gọi G là giao điểm của đường thẳng AB và NF. Chứng minh rằng tam giác GBC cân.

Giải rút gọn:

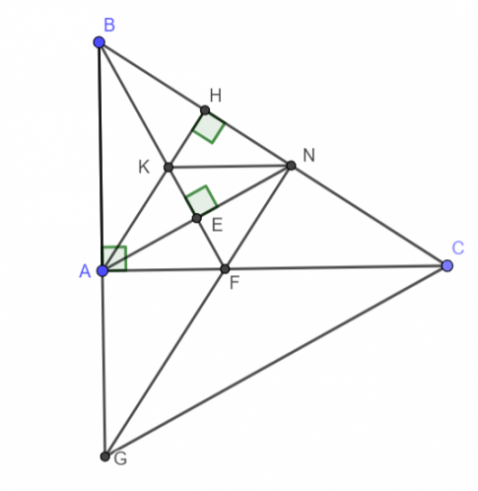
a) BA = BN, chung BE => ∆BEA = ∆BEN (cạnh huyền - cạnh góc vuông).

   => = => BE là tia phân giác

b) ΔBAN có 2 đường cao BE và AH cắt nhau tại K => K là trực tâm

    => NK ⊥ AB mà CA ⊥ AB => NK // CA

c) +) BA = BN, = , chung FB => ∆ABF = ∆NBF (c.g.c)

    => = = 90⁰ 

   +) chung, BA = BN => ∆ABC = ∆NBG (góc nhọn - cạnh góc vuông)

   => BC = BG => ∆BGC cân tại B

Bài 5: Cho tam giác ABC nhọn ( AB < AC), vẽ đường cao AH. Đường trung trực của cạnh BC cắt AC tại M, cắt BC tại N.

a) Chứng minh rằng...

b) Kẻ MI ⊥ AH (I thuộc AH), gọi K là giao điểm của AH với BM. Chứng minh rằng I là trung điểm của AK.

Giải rút gọn:

a) +) M thuộc đường trung trực của BC => MB = MC 

    +) BN = NC , MN chung, BM = CM 

       => ∆MNB  = ∆MNC ( c.c.c) => =

    +) ∆MNC vuông tại N => + = 90°

    +) ∆AHC vuông tại H => + = 90°

     => = => =

b) +) AH ⊥ BC , MI ⊥ AH => BC // MI

    => = (2 góc đồng vị ),  =  (so le trong )

    +) MB = MC => ∆MBC cân tại M => =  

    => =  

    +) chung IM , = => ∆IMA = ∆IMK (góc nhọn - cạnh góc vuông).

      => AI = IK => I là trung điểm của AK.

Bài 6: Cho tam giác nhọn MNP. Các trung tuyến ME và NF cắt nhau tại G. Trên tia đối của tia FN lấy điểm D sao cho FN = FD.

a) Chứng minh rằng ∆ MFN = ∆ PFD.

b) Trên đoạn thẳng FD lấy điểm H sao cho F là trung điểm của HG. Gọi K là trung điểm của PD. Chứng minh rằng 3 điểm M, H, K thẳng hàng.

Giải rút gọn:

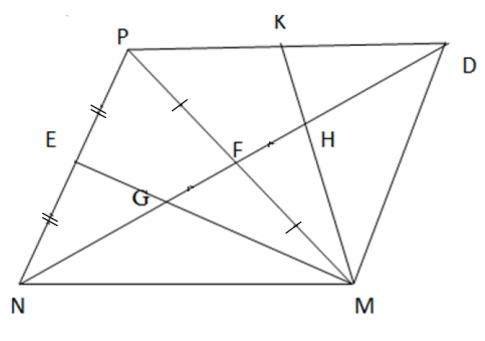
a) MF = PF , =  , FN = FD => ∆FMN = ∆FPD (c.g.c).

b) +) ΔPNM có trung tuyến NF ∩ ME = G => G là trọng tâm => FG = FN

    +) FH = FG, FD = FN => FH = FD => DH = FD

    +) ΔPDM có: DF là trung tuyến,  DH = FD => H là trọng tâm 

     => MH là đường trung tuyến (1)

    +) K là trung điểm của PD => MK là đường trung tuyến  (2)

    Từ (1) và (2) M, H, K thẳng hàng.

Bài 7: Cho tam giác ABC vuông tại A có  AB = AC, AD là tia phân giác của…(D thuộc BC). Gọi E là trung điểm của AC.

a) Chứng minh rằng DE = DB.

b) AB cắt DE tại K. Chứng minh rằng tam giác DCK cân và B là trung điểm của đoạn thẳng AK.

c) AD cắt CK tại H. Chứng minh rằng AH ⊥ CK.

Giải rút gọn:

a) AB = AE, = , chung AD => ∆ADB = ∆ADE (c.g.c) => DB = DE

b) +) ∆ADB = ∆ADE => =   

    +) = 180⁰ - = 180⁰ - =

    +) = , DB = DE, = => ∆DBK = ∆DEC (g.c.g)

   => KD = DC => ∆KDC cân tại D

   +)  ∆DBK = ∆DEC => BK = EC

    +) EC = AE = AC = AB => BK = AB => B là trung điểm của AK

c) +) AB = AK; AB = AC => AK = AC

    +) chung AH, = , AC = AK => ∆HAC = ∆HAK (c.g.c)

   => =  

   mà  + = 180° => = = 90°  => AH ⊥ CK

Bài 8: Ở hình 1, cho biết AE = AF và...Chứng minh rằng AH là đường trung trực của BC.

Giải rút gọn:

+) = => ∆ABC cân tại A 

   => AB = AC => A thuộc đường trung trực của BC (1)

+) FC = AC – AF = AB – AE = BE

+) FC = BE, =  , chung CB => ∆FCB =  ∆EBC (c.g.c)

 =>   =   

 => ∆HBC cân tại H => HB = HC => H thuộc đường trung trực của BC (2)

Từ (1) và (2) => AH là đường trung trực của BC.

Bài 9: Cho tam giác ABC vuông tại A. Tia phân giác của góc C cắt AB tại M. Từ B kẻ BH vuông góc với đường thẳng CM (H thuộc CM). Trên tia đối của HC lấy điểm E sao cho HE = HM.

a) Chứng minh rằng tam giác MBE cân.

b) Chứng minh rằng…

c) Chứng minh rằng EB ⊥ BC.

Giải rút gọn:

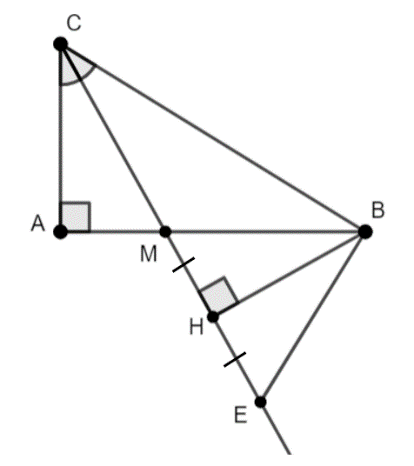
a) MH = EH, chung HB => ∆BHM =  ∆BHE ( 2 cạnh góc vuông)

   => MB = EB => ∆MBE cân tại B

b) +) ∆BHE vuông tại H => = 90° - (1)

    +) ∆AMC vuông tại A => = 90° -  (2)

+) = ; = => = (3)

   Từ (1), (2), (3) => =

c) +) ∆BHM = ∆BHE => = => = 2

    +) CM là đường phân giác của => = 2.

    +) ∆ABC : + = 90° 

   => + 2 = 90⁰ ó + 2 = 90⁰ ó + = 90°

   =>   = 90° => EB ⊥ BC.

Bài 10: Trên đường thẳng a lấy 3 điểm phân biệt I, J, K (J ở giữa I và K). Kẻ đường thẳng b vuông góc với a tại J, trên b lấy điểm M khác điểm J. Đường thẳng qua I vuông góc với MK cắt b tại N. Chứng minh rằng KN vuông góc với MI.

Giải rút gọn:

∆MIK có 2 đường cao MJ, IN cắt nhau tại N

=> N là trực tâm  => KN ⊥ MI.