CHƯƠNG 8: TAM GIÁC

BÀI TẬP CUỐI CHƯƠNG 8

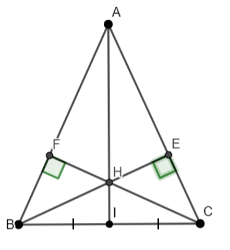
Bài 1: Cho tam giác ABC cân tại A... Hai đường cao BE và CF cắt nhau tại H.

a) Chứng minh rằng ∆ BEC = ∆ CFB.

b) Chứng minh rằng ∆ AHF = ∆ AHE.

c) Gọi I là trung điểm của BC. Chứng minh rằng ba điểm A, H, I thẳng hàng.

Giải nhanh:

a)∆ ABC cân tại A => = và AB = AC => =

BE và CF là hai đường cao của ∆ ABC

=> ∆BEC và  ∆ CFB là 2 tam giác vuông lần lượt tại E và F.

+ Xét ∆BEC vuông tại E và ∆CFB vuông tại F có: BC chung; =

=> ∆ BEC = ∆ CFB (góc nhọn và một cạnh góc vuông)

b) Theo a:  ∆BEC =∆ CFB=> EC = FB 

Có AF = AB – FB;     AE= AC - EC

mà AB = AC, EC = FB => AF = AE

BE và CF là hai đường cao cắt nhau tại H

=> ∆ AFH và  ∆ AEH là 2 tam giác vuông lần lượt tại F và E.

+ Xét ∆ AFH vuông tại F và  ∆AEH vuông tại E  có:  AH chung; AF = AE

=> ∆ AFH = ∆ AEH (cạnh huyền và một cạnh góc vuông).

c) H là giao điểm của 2 đường cao BE và CF trong tam giác ABC

=> H là trực tâm của ∆ ABC => AH ⊥ BC (1)

Có I là trung điểm của BC => AI là đường trung tuyến của ∆ ABC

Xét  ∆ ABI và  ∆ ACI  có: AB = AC; AI chung; IB = IC 

=> ∆ ABI =  ∆ ACI (c.c.c) => =

Có + = 180° => 2 = 180° => = 90° => AI ⊥ BC (2)

Từ (1) và (2) => A, I, H thẳng hàng.

Bài 2: Cho tam giác ABC vuông tại A, vẽ đường cao AH. Trên tia đối của tia HA lấy điểm M sao cho H là trung điểm của AM.

a) Chứng minh tam giác ABM cân.

b) Chứng minh rằng ∆ ABC = ∆ MBC.

Giải nhanh:

a) Có AH là đường cao của ∆ ABC => AH ⊥ BC hay AM ⊥ BH

=> ∆BHA và ∆AHM là 2 tam giác vuông tại H

Xét ∆ BHA và ∆ BHM cùng vuông tại H có : BH chung AH = HM

=> ∆BHA = ∆BHM (hai cạnh góc vuông) => BA = BM  => ∆ABM cân tại B.

b) Theo a: ∆BHA = ∆BHM  => = hay =  

Xét ∆ABC và ∆MBC có :  BC chung; = ; AB = BM

=> ∆ABC = ∆MBC (c.g.c)

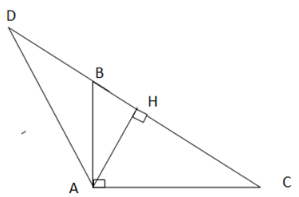
Bài 3: Cho tam giác ABC vuông tại A ( AB , AC), vẽ đường cao AH. Trên tia đối của HC lấy điểm D sao cho HD = DC.

a) Chứng minh AC = AD.

b) Chứng minh rằng  =

Giải nhanh:

a)Ta có AH  là đường cao của ∆ ABC

=>  ∆ AHD và ∆ AHC là 2 tam giác vuông tại H

Xét ∆ AHD và ∆ AHC cùng vuông tại H có : AH chung; HD = HC

=> ∆AHD và ∆AHC (hai cạnh góc vuông) => AC = AD

b) + ∆ABC vuông tại A nên  + = 90°

∆ABH vuông tại H nên + = 90° => =  

+ Có AC = AD => ∆ ACD cân tại A =>   =  

mà  =  =>  =

Bài 4: Cho tam giác vuông ABC vuông tại A (AB < AC). Trên cạnh BC lấy điểm N sao cho BA = BN. Kẻ BE ⊥ AN (E thuộc AN).

a) Chứng minh rằng BE là tia phân giác của góc ABN.

b) Kẻ đường cao AH của tam giác ABC. Gọi K là giao điểm của AH với BE. Chứng minh rằng NK // CA.

c) Đường thẳng BK cắt AC tại F. Gọi G là giao điểm của đường thẳng AB và NF. Chứng minh rằng tam giác GBC cân.

Giải nhanh:

a) Xét ∆ABE và ∆NBE cùng vuông tại E có: AB = BN ;  BE chung

∆ABE = ∆NBE = BE là tia phân giác của góc ABN.

b) Xét tam giác ABN có: AH và BE là hai đường cao cắt nhau tại K

K là trực tâm tam giác ABN NK ⊥ AB

mà AC ⊥ AB NK // AC.

c) Xét ∆FBN và ∆ FBA có :  BN = BA; = ; BF chung

∆FBN và ∆FBA (c.g.c) mà ∆ FBA vuông tại A ∆ FBN vuông tại N

BN ⊥ FN hay BN ⊥ GN ∆ BNG vuông tại N

Xét 2 tam giác vuông ∆BNG và ∆BAC có  BN = BA;  chung

∆BNG = ∆BAC BG = BC ∆ BCG cân tại B.

       = ( 2 góc đồng vị ) Mà ∆MBC cân tại M nên  =   

=  

Xét ∆MIK và ∆MIA cùng vuông tại I có : MI chung; =  

=> ∆MIK = ∆MIA=> IK = IA => I là trung điểm của AK.

Bài 5: Cho tam giác ABC nhọn ( AB < AC), vẽ đường cao AH. Đường trung trực của cạnh BC cắt AC tại M, cắt BC tại N.

a) Chứng minh rằng =  

b) Kẻ MI ⊥ AH (I thuộc AH), gọi K là giao điểm của AH với bM. Chứng minh rằng I là trung điểm của AK.

Giải nhanh:

a) M, N thuộc đường trung trực của BC => MB = MC, NB = NC

=> ∆ MBC cân tại M, N là trung điểm của BC

=> MN là đường trung tuyến của ∆ MBC cân tại M

Xét ∆ MBN  và ∆ MCN có :MB = MC; BN = NC; MN chung

=> ∆ MBN  = ∆ MCN ( c.c.c) => =

∆ AHC vuông góc tại H => + = 90° hay + = 90° (1)

∆ MNC vuông góc tại N =>  + = 90°mà  =

=> hay + = 90° (2)

Từ (1) và (2) ta có : =  

b) Kẻ MI ⊥ AH; AH ⊥ BC => IM // BC=>  =  ( 2 góc so le trong )

      =  ( 2 góc đồng vị )

Mà ∆MBC cân tại M nên  =  =>  = 

Xét ∆MIK và ∆MIA cùng vuông tại I có : MI chung;  =  

=> ∆MIK = ∆MIA => IK = IA => I là trung điểm của AK.

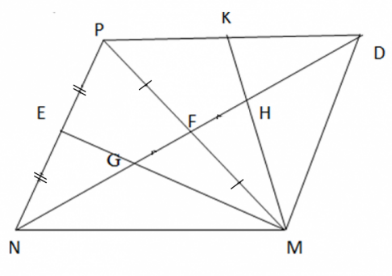
Bài 6: Cho tam giác nhọn MNP. Các trung tuyến ME và NF cắt nhau tại G. Trên tia đối của tia FN lấy điểm D sao cho FN = FD.

a) Chứng minh rằng ∆ MFN = ∆ PFD.

b) Trên đoạn thẳng FD lấy điểm H sao cho F là trung điểm của HG. Gọi K là trung điểm của PD. Chứng minh rằng 3 điểm M, H, K thẳng hàng.

Giải nhanh:

a) ME, NF là trung tuyến của ∆MNP

E là trung điểm của PN, F là trung điểm của PM

Xét ∆ MFN và  ∆ PFD có FN = FD; =  ; FM = FP

 ∆MFN = ∆PFD (c.g.c).

b)+ Trong ∆MNP các trung tuyến ME và NF cắt nhau tại G. G là trọng tâm của ∆MNP FG = FN

mà FG = FH ( F là trung điểm của HG); FN = FD FH = FD => DH = FD

+ Xét tam giác PDM có:  DH = FD mà FD là đường trung tuyến của ∆PDM

=> H là trọng tâm của ∆PDM => MH là đường trung tuyến của ∆PDM (1)

K là trung điểm của PD => MK là đường trung tuyến của ∆PDM (2)

Từ (1) và (2) M, H, K thẳng hàng.

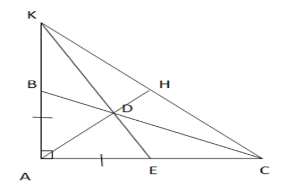
Bài 7: Cho tam giác ABC vuông tại A có  AB = 1/2 AC, AD là tia phân giác của…(D thuộc BC). Gọi E là trung điểm của AC.

a) Chứng minh rằng DE = DB.

b) AB cắt DE tại K. Chứng minh rằng tam giác DCK cân và B là trung điểm của đoạn thẳng AK.

c) AD cắt CK tại H. Chứng minh rằng AH ⊥ CK.

Giải nhanh:

a) Xét ∆ABD và  ∆AED có AD chung; =    ; AB = AE 

=> ∆ ABD =  ∆ AED (c.g.c) => BD = ED

b) + Chứng minh tam giác DCK cân.

Theo a: ∆ ABD =  ∆ AED nên =   

Ta có: + = 180°; + = 180°

Mà =    =

Xét ∆CDE và  ∆KDB có: =    ; DE = DB; =  

 ∆CDE =  ∆KDB (g.c.g) DC = DK ∆DCK cân tại D

+ Chứng minh B là trung điểm của đoạn thẳng AK.

Ta có: ∆CDE = ∆KDB nên EC = KB

mà E là trung điểm của AC nên EC = AE = AC mà AB = AC

KB = AB mà A, B, K thẳng hàng B là trung điểm của AK

c) B là trung điểm của AK AB = AK mà AB = AC AK = AC

Xét ∆KAH và  ∆CAH có: AK = AC; = ; AH chung

∆KAH =  ∆CAH (c.g.c) =  mà + = 180°

=> 2 =  180° => =  90° => AH ⊥ HC hay AH ⊥ CK.

Bài 8: Ở hình 1, cho biết AE = AF và...Chứng minh rằng AH là đường trung trực của BC

Giải nhanh:

=  => ∆ ABC cân tại A => AB = AC => A thuộc đường trung trực của BC (1)

Ta có: FC = AC – AF;    EB = AB -  AE Mà AB = AC, AE= AF FC = CB

Xét ∆ FCB và  ∆ EBC có: BC chung; =  ; FC = CB 

∆FCB =  ∆EBC (c.g.c) =  ∆HCB cân tại H HC = HB 

H thuộc đường trung trực của BC (2)

Từ (1) và (2) AH là đường trung trực của BC.

Bài 9: Cho tam giác ABC vuông tại A. Tia phân giác của góc C cắt AB tại M. Từ B kẻ BH vuông góc với đường thẳng CM (H thuộc CM). Trên tia đối của HC lấy điểm E sao cho HE = HM.

a) Chứng minh rằng tam giác MBE cân.

b) Chứng minh rằng =

c) Chứng minh rằng EB ⊥ BC.

Giải nhanh:

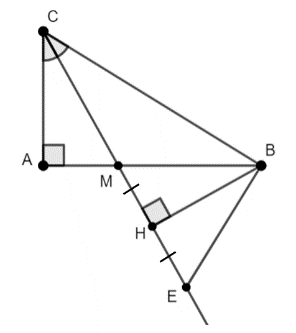
a) BH ⊥ CM => ∆BHM và  ∆BHE là 2 tam giác vuông tại H

Xét ∆BHM và  ∆BHE cùng vuông tại H có:  BH chung; HM = HE

=> ∆BHM =  ∆BHE (hai cạnh góc vuông) => MB = BE => ∆MBE cân tại B

b) Xét ∆CAM vuông tại A nên + = 90°

Xét ∆BHE vuông tại H nên + = 90°

mà = ;   =  => =

c) + Theo b có: ∆BHM = ∆BHE nên =

Có + = => 2 =  

+ CM là đường phân giác của => = = 

Hay 2 =

+ Xét ∆ABC vuông tại A =>  + = 90°

=> 2 + = 90°=> 2 + = 90°

=> + = 90°. =>  = 90° => EB ⊥ BC.

Bài 10: Trên đường thẳng a lấy 3 điểm phân biệt I, J, K (J ở giữa I và K). Kẻ đường thẳng b vuông góc với a tại J, trên b lấy điểm M khác điểm J. Đường thẳng qua I vuông góc với MK cắt b tại N. Chứng minh rằng KN vuông góc với MI.

Giải nhanh:

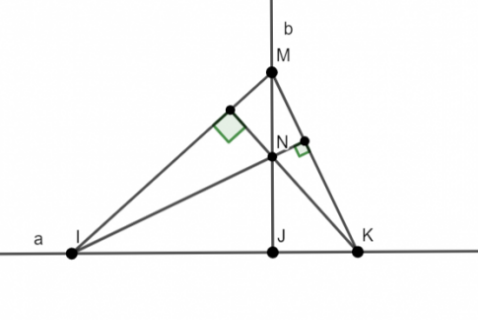
+ Ta có đường thẳng b vuông góc với đường thẳng a tại J => MJ ⊥ IK

=> MJ là đường cao của ∆ IMK

+ IN ⊥ MK => IN là đường cao của ∆IMK

+ Xét ∆IMK có: MJ, IN là 2 đường cao giao nhau tại N => N là trực tâm của ∆ IMK  => KN ⊥ MI.