CHƯƠNG 8: TAM GIÁC

BÀI 8: TÍNH CHẤT BA ĐƯỜNG CAO CỦA TAM GIÁC

1. ĐƯỜNG CAO CỦA TAM GIÁC

Bài 1: Em hãy vẽ một tam giác ABC trên giấy, sau đó dùng êke vẽ đoạn thẳng vuông góc từ đỉnh B đến cạnh đối diện AC của tam giác.

Giải nhanh:

Bài 2: Vẽ ba đường cao AH, BK, CE của tam giác nhọn ABC

Giải nhanh:

Bài 3: Vẽ đường cao xuất phát từ đỉnh B của tam giác vuông ABC ( Hình 2a). Vẽ đường cao xuất phát từ đỉnh F của tam giác tù DEF ( Hình 2b).

Giải nhanh:

a) Đường cao từ đỉnh B của tam giác ABC là BA (vì BA vuông AC).

b) 

2. TÍNH CHẤT BA ĐƯỜNG CAO CỦA TAM GIÁC

Bài 1: Vẽ một tam giác rồi dùng êke vẽ ba đường cao của tam giác ấy (Hình 3). Em hãy quan sát và cho biết các đường cao vừa vẽ có cùng đi qua một điểm hay không.

Giải nhanh:

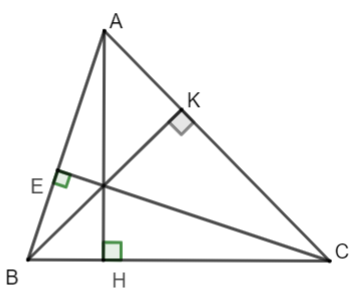 Cả 3 đường cao đều cùng đi qua một điểm.

Bài 2: Cho tam giác LMN có hai đường cao LP và MQ cắt nhau tại S (Hình 6). Chứng minh rằng NS vuông góc ML.

Giải nhanh:

Trong tam giác MNL  có :

LP ⊥ MN LP là đường cao của tam giác MNL.

MQ ⊥ LN MQ là đường cao của tam giác MNL.

LP giao với MQ tại S S là trực tâm của tam giác MNL

Vì 3 đường cao của tam giác cắt nhau tại 1 điểm. NS ⊥ LM.

Bài 3: Cho tam giác ABC có ba đường cao AD, BE, CF đồng quy tại trực tâm H. Tìm trực tâm của các tam giác HBC, HAB, HAC.

Giải nhanh:

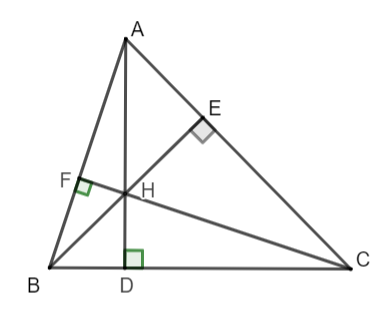
+ Xét ∆ HBC có HD ⊥BC;  CE ⊥BH; BF ⊥ CH

Tam giác HBC có 3 đường cao là HD, CE, BF.

Mà BF, DH, CE giao nhau tại A A là trực tâm của ∆ HBC.

+ Xét ∆ HAB có HF ⊥AB; AE ⊥ BH; BD ⊥ AH

Tam giác HAB có 3 đường cao là HF, AE, BD.

Mà BD, FH, AE giao nhau tại C C là trực tâm của ∆ HAB.

+ Xét ∆ HAC có HE ⊥AC; AF ⊥ CH; CD ⊥ AH

Tam giác HAC có 3 đường cao là HE, AF, CD.

AF, HE, CD giao nhau tại B B là trực tâm của ∆ HAC.

BÀI TẬP

Bài 1: Cho tam giác ABC vuông tại A. Lấy điểm H thuộc cạnh AB. Vẽ HM vuông góc với BC tại M. Tia MH cắt tia CA tại N. Chứng minh rằng  CH vuông góc với NB.

Giải nhanh:

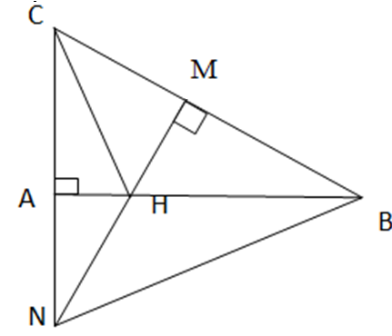
Xét tam giác CNB có :

BA ⊥ CA hay BA ⊥ CN BA là đường cao của tam giác CNB

HM ⊥ CB hay NM ⊥ CB NM là đường cao của tam giác CNB

NM giao với BA tại điểm H H là trực tâm của tam giác CNB CH ⊥ NB

Bài 2: Cho tam giác ABC vuông tại A. Trên tia BA lấy điểm M sao cho BM = BC. Tia phân giác của góc B cắt AC tại H. Chứng minh rằng MH vuông góc với BC.

Giải nhanh:

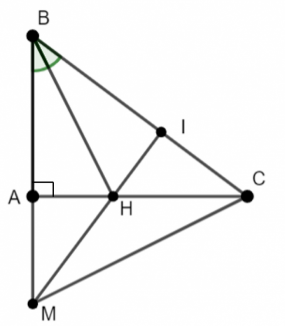
Gọi MH giao với BC tại điểm I.

+ Xét  ∆MBH và  ∆CBH có: MB = MC; = ; BH chung

∆MBH = ∆CBH (c.g.c) =  

+ Xét tam giác ABC vuông tại A có:  + = 90°

+ Ta có:  + =  + =  90°

+ Xét tam giác BMI có: + = 90°   = 90°.

MI ⊥ BC hay MH vuông góc với BC.

Bài 3: Cho tam giác ABC vuông cân tại A. Lấy điểm E thuộc cạnh AC. Trên tia đối của tia AB lấy điểm D sao cho AD = AE. Chứng minh rằng:

a) DE vuông góc với BC.

b) BE vuông góc với DC.

Giải nhanh:

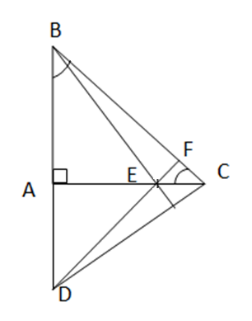
a) Gọi F là giao điểm của DE và BC

+ AD = AE ∆ADE cân tại A

∆ABC vuông cân tại A => BA ⊥ AC hay EA ⊥ AD ∆ ADE vuông cân tại A

= = 45°

+ ∆ ABC vuông cân tại A = = 45°

+ Xét ∆EFC có : + + = 180°   45° + 45° + = 180°

= 180° - 90° = 90°  EF ⊥ BC hay DE ⊥ BC.

b) Xét tam giác BCD có: 

CA ⊥ BD CA là đường cao của ∆ BCD

DE ⊥ BC DE là đường cao của ∆ BCD

Mà DE giao với CA tại E E là trực tâm của ∆ BCD BE ⊥ CD.

Bài 4: Cho tam giác nhọn ABC có ba đường cao AD, BE, CF. Biết AD = BE = CF. Chứng minh rằng tam giác ABC đều.

Giải nhanh:

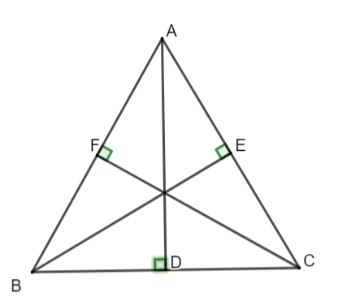
BE là đường cao của ∆ ABC => ∆ ABE vuông tại E.

CF là đường cao của ∆ ABC => ∆ AFC vuông tại F.

AD là  đường cao của ∆ ABC => ∆ ADC vuông tại D.

+ Xét ∆ ABE vuông tại E và ∆ AFC vuông tại F có : BE = CF;  chung

=> ∆ ABE = ∆ AFC (góc nhọn và một cạnh góc vuông).=> AB = AC (1)

+ Xét ∆CDA vuông D và ∆ AFC vuông F có :AC chung; AD = CF

=> ∆CDA = ∆AFC=> = => ∆ ABC cân tại B => AB = BC (2)

Từ (1), (2) ta có : AB = AC = BC => ∆ ABC đều.