CHƯƠNG 8: TAM GIÁC

BÀI 1: GÓC VÀ CẠNH CỦA MỘT TAM GIÁC

1. TỔNG SỐ ĐO BA GÓC CỦA MỘT TAM GIÁC

Bài 1: a. Cắt một tấm bìa hình tam giác và tô màu ba góc của nó (Hình 1a). Cắt rời ba góc ra khỏi tam giác rồi đặt ba góc kề nhau (Hình 1b). Em hãy dự đoán tổng số đo của ba góc trong hình 1b.

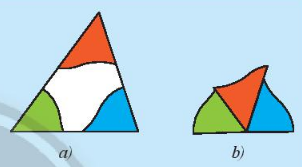
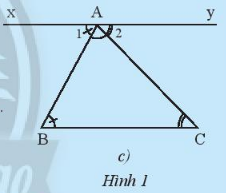
b. Chứng minh tính chất về tổng số đo ba góc trong một tam giác theo gợi ý.

Giải nhanh:

a) bằng 180^o 

b) Qua A kẻ đường thẳng xy song song với BC như hình 1c.

Ta có xy // BC (so le trong) (1) và (so le trong ) (2)

Từ (1) và (2) suy ra: + + =

Bài 2: Tìm số đo các góc chưa biết cả các tam giác trong Hình 3 và cho biết tam giác nào là tam giác nhọn, tam giác tù, tam giác vuông.

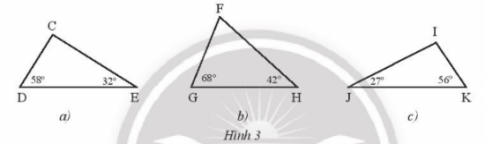
Giải nhanh:

 a) Xét tam giác CDE có:

.

Tam giác CDE là tam giác vuông.

b) Xét tam giác GHF có: .

Tam giác FGH là tam giác nhọn.

c. Xét tam giác IJK có: .

Tam giác IJK là tam giác tù.

2. QUAN HỆ GIỮA BA CẠNH CỦA MỘT TAM GIÁC

Bài 1: Hãy so sánh tổng độ dài hai cạnh của tam giác trong Hình 4 với độ dài cạnh còn lại

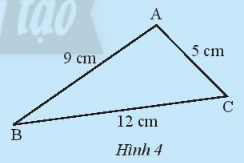
Giải nhanh:

Ta có: AB + BC = 9 + 12 = 21, ⇒ AB + BC > AC.

Tương tự, AB + AC > BC; AC + BC > AB.

Bài 2: Trong các bộ ba độ dài đoạn thẳng dưới đây, bộ ba nào có thể là độ dài ba cạnh của một tam giác?

a. 7cm; 8cm; 11cm        b. 7cm; 9cm; 16cm        c. 8cm; 9cm; 16cm

Giải nhanh:

Có hai bộ ba có thể là độ dài ba cạnh của một tam giác là: a và c.

Bài 3: Cho tam giác ABC với độ dài ba cạnh là ba số nguyên. Nếu biết AB = 5cm, AC = 3cm thì cạnh BC có thể có độ dài là bao nhiêu xăng ti mét?

Giải nhanh:

Ta có: 5 - 3 < BC < 5 + 3, hay 2 < BC < 8.

Vậy độ dài cạnh BC có thể là: 3 cm, 4 cm, 5 cm, 6 cm, 7 cm.

BÀI TẬP

Bài 1: Tìm số đo các góc chưa biết của các tam giác trong Hình 5.

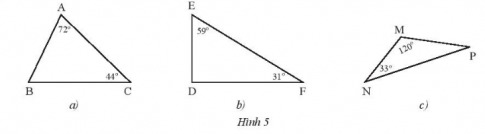
Giải nhanh:

a) .            b) .

c) .

Bài 2: Tìm số đo của góc x trong Hình 6

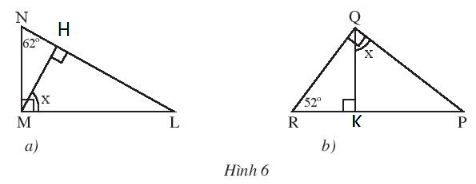
Giải nhanh:

a) Gọi H là chân vuông góc kẻ từ M xuống cạnh NL.

.

Vậy x = .

b) Gọi K là chân đường vuông góc kẻ từ Q xuống cạnh RP.

Xét tam giác QRK có nên

Vì .

Bài 3: Hãy chia tứ giác ABCD trong hình 7 thành hai tam giác để tính tổng số đo của bốn góc A, B, C, D

Giải nhanh:

Xét tam giác ABD có: .

Xét tam giác BDC có: .

= .

Bài 4: Trong các bộ ba độ dài đoạn thẳng dưới đây, bộ ba nào có thể là độ dài ba cạnh của một tam giác?

a) 4cm, 5cm, 7cm

b) 2cm, 4cm, 6cm

c) 3cm, 4cm, 8cm

Giải nhanh:

bộ ba câu a) 4cm, 5cm, 7cm có thể là độ dài ba cạnh của một tam giác.

Bài 5: Cho tam giác ABC có BC = 1cm, AB = 4cm. Tìm độ dài cạnh AC (theo đơn vị cm), biết rằng độ dài này là một số nguyên. 

Giải nhanh:

Áp dụng đính lí về độ dài 3 cạnh của một tam giác ta có: 4 - 1 < AC <  4 + 1, hay 3 < AC < 5.

Vì độ đài AC là một số nguyên, nên độ dài AC có thể là: 4.

Bài 6: Trong một trường học, người ta đánh dấu ba khu vực A, B, C là ba đỉnh của một tam giác, biết khoảng cách AC = 15m, AB = 45m.

a. Nếu đặt ở khu vực C một thiết bị phát wifi có bán kính hoạt động 30m thì tại khu vực B có nhận được tín hiệu không? Vì sao?

b. Cũng câu hỏi như trên với thiết bị phát wifi có bán kính hoạt động 60m.

Giải nhanh:

45 - 15 < BC < 45 + 15, hay 30 < BC < 60.

a) Nếu đặt ở khu vực C một thiết bị phát wifi có bán kính hoạt động 30 m thì khu vực B không nhận được tín hiệu vì BC > 30 m.

b) Nếu đặt ở C một thiết bị phát wifi có bán kính hoạt động 60 m thì khu vực B nhận được tín hiệu vì BC < 60 m.