1. TỔNG SỐ ĐO BA GÓC CỦA MỘT TAM GIÁC

HĐKP1:

a) Tổng số đo 3 góc bằng 180°

b) Qua A kẻ đường thẳng xy song song với BC như hình 1c.

Ta có xy // BC $\widehat{B}=\widehat{xAb}$ (so le trong) (1)

và $\widehat{C}=\widehat{yAC}$ (so le trong) (2)

Từ (1) và (2) suy ra:

$\widehat{B}+\widehat{BAC}+\widehat{C}=\widehat{A_{1}}+\widehat{BAC}+\widehat{A_{2}}=\widehat{xAy}=180°$

⇒ Định lí:

Tổng số đo ba góc của một tam giác bằng 180°.

Ví dụ 1: SGK – tr 44, 45

Chú ý: 

- Tam giác có 3 góc nhọn được gọi là tam giác nhọn.

- Tam giác có 1 góc vuông được gọi là tam giác vuông, cạnh đối diện góc vuông gọi là cạnh huyền, hai cạnh còn lại gọi là hai cạnh góc vuông.

- Tam giác có 1 góc tù được gọi là tam giác tù.

Thực hành 1: 

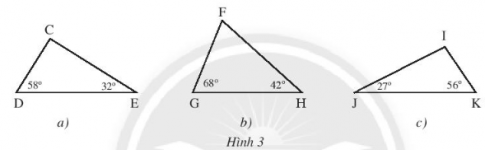
a) Xét tam giác CDE có:

$\widehat{C}+\widehat{D}+\widehat{E}=180°$ (ĐL tổng 3 góc trong 1 tam giác)

=> $\widehat{C}=180°-\widehat{D}-\widehat{E}=180°-58°-32°=90°$

Tam giác CDE là tam giác vuông.

b) Xét tam giác GHF có: 

$\widehat{F}+\widehat{G}+\widehat{H}=180°$

=> $\widehat{F}=180°-\widehat{G}-\widehat{H}=180°-68°-45°=70°$

Tam giác FGH là tam giác nhọn.

c. Xét tam giác IJK có: $\widehat{I}+\widehat{J}+\widehat{K}=180°$

=> $\widehat{I}=180°-\widehat{J}-\widehat{K}=180°-27°-56°=97°$

Tam giác IJK là tam giác tù.

Nhận xét: 

Trong một tam giác vuông, tổng hai góc nhọn bằng 90°.

2. QUAN HỆ GIỮA BA CẠNH CỦA MỘT TAM GIÁC

HĐKP2:

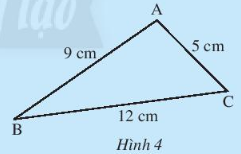
Ta có: AB + BC = 9 + 12 = 21, ⇒ AB + BC > AC.

Tương tự, AB + AC > BC; AC + BC > AB.

Vậy tổng độ dài hai cạnh bất kì lớn hơn độ dài cạnh còn lại.

=> Định lí:

Trong một tam giác, tổng độ dài hai cạnh bất kì bao giờ cũng lớn hơn độ dài cạnh còn lại.

Nhận xét: 

Trong một tam giác độ dài một cạnh bao giờ cũng lớn hơn hiệu và nhỏ hơn tổng độ dài hai cạnh còn lại.

Lưu ý: 

Khi xét độ dài ba đoạn thẳng có thỏa mãn các bất đẳng thức tam giác hay không, ta chỉ cần so sánh độ dài lớn nhất với tổng của hai độ dài còn lại, hoặc so sánh độ dài nhỏ nhất với hiệu của hai độ dài còn lại.

Thực hành 2.

Ta có: 

a. 8 - 7 < 11 < 7 + 8.

b. 16 = 7 + 9.

c. 9 - 8 < 16 < 8 + 9.

Có hai bộ ba có thể là độ dài ba cạnh của một tam giác là: a và c.

Vận dụng:

Theo định lí về quan hệ giữa độ dài 3 cạnh của một tam giác ta có:

5 - 3 < BC < 5 + 3, hay 2 < BC < 8.

Mà độ dài cạnh BC là một số nguyên, nên độ dài cạnh BC có thể là: 3; 4; 5; 6; 7.

Thử lại các giá trị cạnh BC vừa tìm được ở trên (ta so sánh độ dài cạnh lớn nhất với tổng hai độ dài còn lại hoặc độ dài cạnh nhỏ nhất với hiệu độ dài hai cạnh còn lại) thì thấy thỏa mãn.

Vậy độ dài cạnh BC có thể là: 3 cm, 4 cm, 5 cm, 6 cm, 7 cm.