CHƯƠNG 8: TAM GIÁC

BÀI 7: TÍNH CHẤT BA ĐƯỜNG TRUNG TUYẾN CỦA TAM GIÁC

1. ĐƯỜNG TRUNG TUYẾN CỦA TAM GIÁC

Bài 1: Vẽ tam giác ABC, xác định trung điểm D của cạnh BC và vẽ đoạn thẳng nối hai điểm A và D.

Giải nhanh:

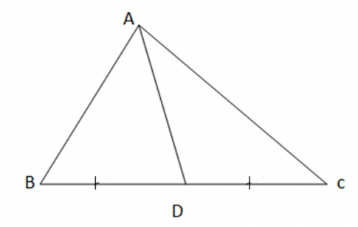
Bài 2: Vẽ tiếp các đường trung tuyến còn lại của tam giác ABC (hình 1).

Giải nhanh:

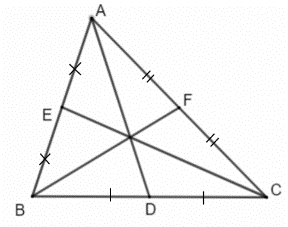
Bài 3: a) Vẽ đường trung tuyến DH của tam giác DEF (Hình 2).

b) Vẽ đường trung tuyến MK của tam giác vuông MNP ( Hình 3).

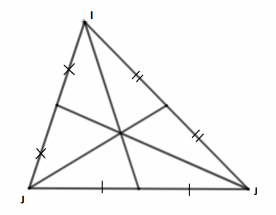
c) Vẽ tam giác nhọn IJK và tất cả các đường trung tuyến của nó.

Giải nhanh:

a) 

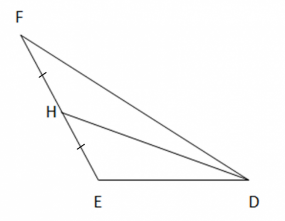
b)

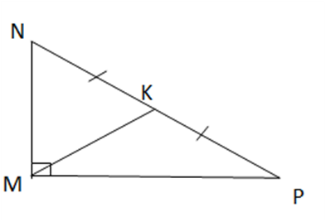
c)

2. TÍNH CHẤT BA ĐƯỜNG TRUNG TUYẾN CỦA TAM GIÁC

Bài 1: a) Cắt một tam giác bằng giấy. Gấp lại để xác định trung điểm một cạnh của nó. Kẻ đoạn thẳng nối trung điểm này với đỉnh đối diện ( Hình 4). Bằng cách tương tự, hãy vẽ tiếp hai đường trung tuyến còn lại. Quan sát tam giác trên hình, em thấy ba đường trung tuyến vừa vẽ có cùng đi qua một điểm hay không 

b) Em hãy đếm ô rồi vẽ lại tam giác ABC trong Hình 5 vào giấy kẻ ô vuông. Vẽ hai đường trung tuyến BE và CF  của tam giác ABC. Hai đường trung tuyến này cắt  nhau tại G . Tia AG cắt BC tại D. Em hãy quan sát và cho biết

• AD có phải đường trung tuyến của tam giác ABC không
• Các tỉ số 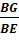; ; 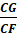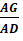bằng bao nhiêu ?

Giải nhanh:

a)

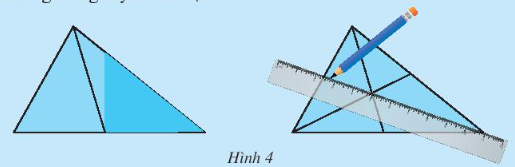
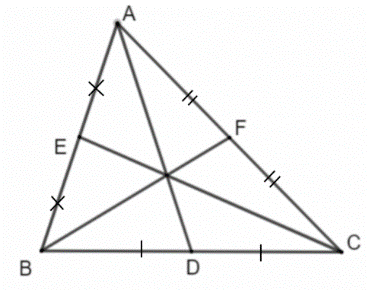
Ta thấy: cả 3 đường trung tuyến đều cùng đi qua một điểm.

b)

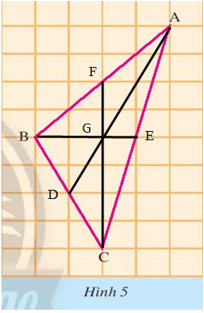
AD chính là đường trung tuyến của tam giác ABC; = = =

Bài 2: Trong Hình 7, G là trọng tâm của tam giác AEF và đường trung tuyến AM. Hãy tính các tỉ số…

Giải nhanh:

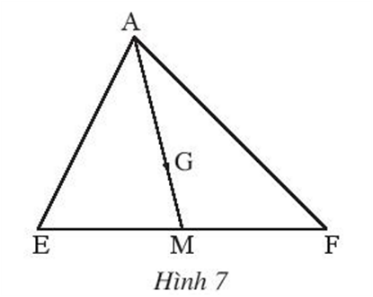
G là trọng tâm của tam giác ABC, AM là đường trung tuyến cuả tam giác ABC

=     AG = AM

a) Ta có : AG + GM = AM AM + GM = AM GM = AM  =

b) Ta có : AG + GM = AM AG + GM = 3GM AG = 2 GM  =

c)  =     = 2

Bài 3: Cho tam giác ABC có O là trung điểm của BC, trên tia đối của tia OA, lấy điểm D sao cho OA = OD. Gọi I và J lần lượt là trọng tâm tam giác ABC và DBC. Chứng minh rằng AI = IJ = JD.

Giải nhanh:

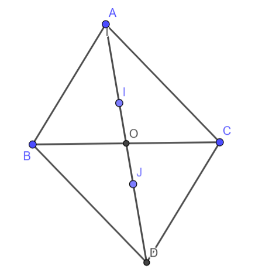
Vì I là trọng tâm của tam giác ABC, AO là đường trung tuyến của tam giác ABC

 = , = .

Vì J là trọng tâm của tam giác DBC, DO là đường trung tuyến của DBC

 = , = .

Có OA = OD AI = JD, IO = JO O là trung điểm của IJ

Ta có : OA = AI + OI OA = AI + IJ  OA = OA + IJ  OA = IJ 

IJ = OA AI = IJ = JD.

BÀI TẬP

Bài 1: Quan sát Hình 8. Thay ? bằng số thích hợp

EG = ..?... EM , GM = ..?.. EM,  GM = ..?.. EG,  FG = ..?.. GN,  FN = ..?.. GN,  FN = ..?.. FG

Giải nhanh:

EG = EM; GM = EM; GM = GE; FG = 2GN; FN = 3GN; FN =  FG

Bài 2: Quan sát hình 9

a) Biết AM = 15 cm, tính AG                     b) Biết GN = 6 cm, tính CN

Giải nhanh:

Trong tam giác ABC có AM, NC là hai đường trung tuyến

G là giao điểm của AM, NCG là trọng tâm của tam giác ABC

a) AG = AM AG = . 15 AG = 10

b) GN = .CN 6 = .CN CN = 6. 3 = 18

Bài 3: Cho tam giác ABC. Hai đường trung tuyến AM và CN cắt nhau tại G. Trên tia đối của tia AM lấy điểm E sao cho ME = MG.

a) Chứng minh rằng BG song song với EC.

b) Gọi I là trung điểm của BE, AI cắt BG tại F. Chứng minh AF = 2 FI.

Giải nhanh:

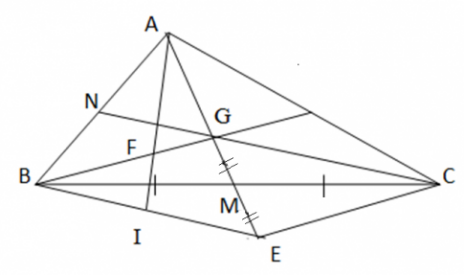
a) Xét  ∆BMG và  ∆CME ta có: BM = CM;  = ; ME = MG 

∆ BMG = ∆ CME (c.g.c)  = ;

Mà hai góc ở vị trị so le trong GB // CE.

b) Xét tam giác ABC có AM và CN là hai đường trung tuyến cắt nhau tại G

G là trọng tâm của tam giác ABC AG = 2GM

+ Ta có: GE = GM + EM GE = 2GM (GM = EM) AG = GE

G là trung điểm đoạn thẳng AE BG là đường trung tuyến của tam giác ABM.

+ Xét tam giác ABM có: AI và BG là 2 đường trung tuyến

mà AI cắt BG tại F F là trọng tâm của tam giác ABC AF = 2FI

Bài 4: Cho tam giác ABC cân tại A có BM và CN là hai đường trung tuyến.

a) Chứng minh rằng BM = CN.

b) Gọi I là giao điểm của BM và CN, đường thẳng AI cắt BC tại H. Chứng minh H là trung điểm BC.

Giải nhanh:

a) ∆ ABC cân tại A  AB = AC  

N trung điểm AB => AN = NB = AB; M trung điểm AC => AM = MC = AC

AN = AM

Xét ∆ ANC và ∆ AMB ta có: AB = AC;  chung; AN = AM 

 ∆ ANC = ∆ AMB (c.g.c) NC = MB

b) 2 đường trung tuyến BM và CN cắt nhau tại I

I là trọng tâm của ∆ ABC IB = BM,  IC = CN

mà BM = CN IB = IC

+ Xét ∆ ACI và ∆ ABI có :  AB = AC; AI chung; IB = IC

∆ ACI = ∆ ABI (c.c.c)  =  

+ Xét ∆ ABH và ∆ ACH có :  AB = AC;  = ; AH chung

∆ ABH = ∆ ACH (c.g.c). BH = CH H là trung điểm của BC.

Bài 5: Cho tam giác ABC có đường trung tuyến BM bằng đường trung tuyến CN. Chứng minh rằng tam giác ABC cân

Giải nhanh:

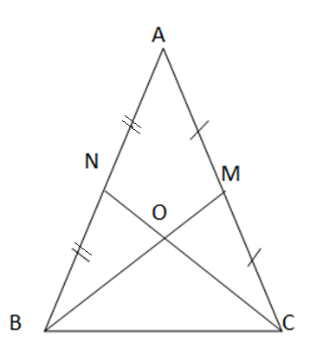
Gọi O là giao điểm của BM và CN O là trọng tâm của tam giác ABC

CO = CN, BO = BM mà BM = CN CO = BO ∆ OBC cân tại O

=  hay  =  

Xét  ∆ NBC và  ∆ MBC ta có: CN = BM; = ; BC chung 

∆ NBC =  ∆ MBC ( c.g.c ) = hay =  

∆ ABC cân tại A.

Bài 6: Cho tam giác ABC cân tại A có BE và CD là hai đường trung tuyến cắt nhau tại F ( Hình 10). Biết BE = 9 cm, tính độ dài đoạn thẳng DF

Giải nhanh:

+ ∆ ABC cân tại A AB = AC

D là trung điểm của AB AD = E là trung điểm của AC AE = AC

AD = AE

+ Xét ∆ ABE và ∆ ACD có : AB = AC;  chung ; AE = AD

∆ ABE = ∆ ACD ( c.g.c) BE = CD = 9 cm

+ Xét  ∆ ABC có hai đường trung tuyến BE và CD cắt nhau tại F

F là trọng tâm của tam giác ABC DF = DC DF =  .9 = 3 cm.