Câu 1: Cho hình vẽ như bên dưới. Biết AM = 12 cm. Tính chiều dài của đoạn thẳng AG.

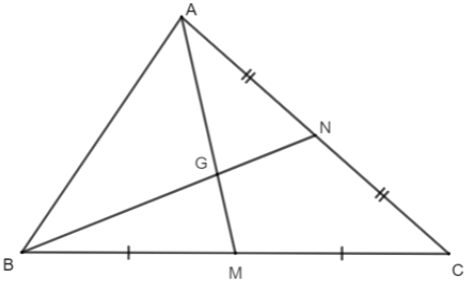
• A. 10 cm;
• B. 4 cm;
• C. 6 cm;

• D. 8 cm.

Câu 2: Cho tam giác ABC có M, N lần lượt là trung điểm của BC và AC, AM và BN cắt nhau tại G. Tỉ số $\frac{AG}{AM}$ bằng :

• A. $\frac{2}{3}$

• B. $\frac{1}{3}$
• C. $\frac{3}{4}$
• D. $\frac{3}{2}$

Câu 3: Cho tam giác ABC có M, N lần lượt là trung điểm của BC và AC, AM và BN cắt nhau tại G. Tỉ số $\frac{GM}{AG}$ bằng :

• A. $\frac{2}{3}$
• B. $\frac{1}{3}$
• C. $\frac{3}{4}$

• D. $\frac{3}{2}$

Câu 4: Cho hình vẽ như bên dưới. Biết GN = 4 cm. Độ dài đoạn thẳng BN bằng:

• A. 12 cm;

• B. 10 cm;
• C. 14 cm;
• D. 16 cm.

Câu 5: Cho tam giác ∆ABC cân tại A có hai điểm E và F lần lượt là trung điểm của AC và AB. Khi đó tam giác GBC là:

• A. Tam giác cân;

• B. Tam giác thường;
• C. Tam giác đều;
• D. Tam giác vuông.

Câu 6: Cho tam giác ∆ABC có đường trung tuyến BD bằng đường trung tuyến CF. Khi đó tam giác ∆ABC là:

• A.Tam giác vuông;
• B. Tam giác vuông cân;
• C.Tam giác thường;

• D.Tam giác cân.

Câu 7: Cho tam giác ∆ABC, điểm M thuộc đoạn thẳng BC sao cho BM = 2MC. Trên tia đối của tia CA lấy điểm D sao cho CD = CA. Gọi E là giao điểm của AM và BD. Khi đó điểm M là:

• A. Trọng tâm của ΔABD;

• B. Trọng tâm của ΔABC;
• C. Trực tâm của ΔABC;
• D. Cách đều ba đỉnh của ΔABD.

Câu 8: Điền vào chỗ trống sau: “Đường trung tuyến của tam giác là đoạn thẳng nối một đỉnh của tam giác với ... của cạnh đối diện”.

• A. Trung trực;

• B. Trung điểm;

• C. Trọng tâm;
• D. Giao điểm.

Câu 9: Cho tam giác ΔABC có đường trung tuyến AD, trên đoạn thẳng AD lấy điểm E và F sao cho AE = EF = FD. Điểm F là:

• A. Trọng tâm của ΔABC;

• B. Trực tâm của ΔABC;
• C. Cách đều ba đỉnh của ΔABC;
• D. Cách đều ba cạnh của ΔABC.

Câu 10: Chọn phát biểu đúng:

• A. Đường trung tuyến của tam giác là đoạn thẳng đi qua trung điểm và vuông góc với cạnh của tam giác tại trung điểm ấy;
• B. Ba đường trung tuyến của tam giác đi qua một điểm, điểm đó cách mỗi đỉnh một khoảng bằng $\frac{1}{3}$ độ dài đường trung tuyến đi qua đỉnh ấy;

• C. Ba đường trung tuyến của tam giác đi qua một điểm, điểm đó cách mỗi đỉnh một khoảng bằng $\frac{2}{3}$ độ dài đường trung tuyến đi qua đỉnh ấy;

• D. Giao điểm của ba đường trung tuyến trong một tam giác cách đều ba đỉnh của tam giác đó.

Câu 11: Điền vào chỗ trống sau: “Ba đường trung tuyến của một tam giác cắt nhau tại một điểm. Điểm đó cách mỗi đỉnh một khoảng bằng … độ dài đường trung tuyến đi qua điểm ấy.”

• A. $\frac{1}{3}$
• B. $\frac{1}{2}$

• C. $\frac{2}{3}$

• D. $\frac{1}{4}$

Câu 12: Cho tam giác ABC có M, N lần lượt là trung điểm của BC và AC, AM và BN cắt nhau tại G. Tỉ số $\frac{GM}{AM}$ bằng :

• A. $\frac{2}{3}$

• B. $\frac{1}{3}$

• C. $\frac{3}{4}$
• D. $\frac{3}{2}$

Câu 13: Cho ∆ABC có hai đường trung tuyến BD và CF cắt nhau tại G. Biết BD = CF và AG cắt BC tại E. Số đo góc AEC là :

• A. 30°;
• B. 45°;
• C. 60°;

• D. 90°.

Câu 14: Cho hình như bên dưới. Đường thẳng AM trong hình bên dưới là:

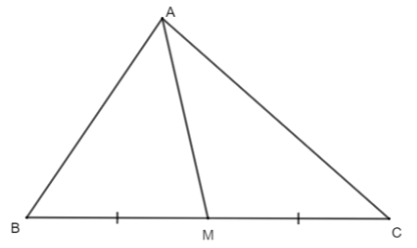
• A. Đường trung trực của tam giác ∆ABC;

• B. Đường trung tuyến của tam giác ∆ABC;

• C. Đường cao của tam giác ∆ABC;
• D. Đường phân giác của tam giác ∆ABC.

Câu 15: Cho các hình vẽ sau:

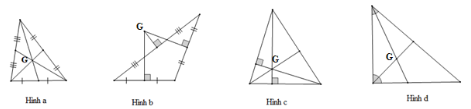
Điểm G trong hình nào là trọng tâm của tam giác đó?

• A. Hình a;

• B. Hình b;
• C. Hình c;
• D. Hình d.

Câu 16: Một tam giác có tất cả bao nhiêu đường trung tuyến?

• A. 1;
• B. 2;

• C. 3;

• D. 4.

Câu 17: Giao điểm của ba đường trung trực của một tam giác:

• A. Là trực tâm của tam giác đó;
• B. Cách đều ba đỉnh của tam giác đó;

• C. Là trọng tâm của tam giác đó;

• D. Cách đều ba cạnh của tam giác đó.

Câu 18: Cho tam giác DEF có trung tuyến DM và trọng tâm G. Khẳng định nào sau đây là sai?

• A. DG = 2GM;
• B. $DG=\frac{2}{3}DM$
• C. $GM=\frac{1}{3}DM$

• D. $DM=\frac{3}{2}GM$

Câu 19: Cho tam giác ABC cân tại A có hai đường trung tuyến BD và CF cắt nhau tại G. Biết BD = 9 cm. Độ dài đoạn thẳng GF bằng:

• A. 6 cm;

• B. 3 cm;

• C. 4 cm;
• D. 5 cm.

Câu 20: Cho hình vẽ sau:

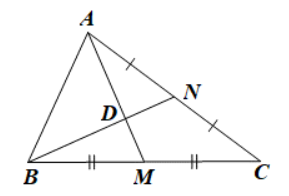
Biết AM = 3 cm, độ dài đoạn thẳng AD bằng

• A. 1 cm;

• B. 2 cm;

• C. 3 cm;
• D. 4 cm.