Câu 1: Hãy phát biểu phần còn thiếu của kết luận trong định lí sau: Nếu một đường thẳng cắt hai đường thẳng song song thì hai góc so le trong ...

• A. song song;

• B. cắt nhau;
• C. bằng nhau;
• D. vuông góc;

Câu 2: Điền vào chỗ chấm phần kết luận để hoàn thành định lí sau:

Nếu một đường thẳng cắt hai đường thẳng song song thì hai góc so le trong …

• A. Bằng nhau;

• B. Kề nhau;
• C. Phụ nhau;
• D. Kề bù nhau.

Câu 3: ChọnCâu sai. Điền vào chỗ trống bằng những nội dung thích hợp để được các định lí: “Nếu tia Ot là tia phân giác của góc xOy thì …”

• A. Ot nằm giữa hai tia Ox và Oy;
• B. $\widehat{xOt}=\widehat{tOy}$
• C. $\widehat{xOt}=\widehat{tOy}=\frac{\widehat{xOy}}{2}$

• D. $\widehat{xOt}=\widehat{tOy}=\widehat{xOy}$

Câu 4: Phát biểu bằng lời định lí sau:

• A. Nếu một đường thẳng vuông góc với một trong hai đường thẳng song song thì nó vuông góc với đường thẳng kia

• B.Nếu một đường thẳng vuông góc với một trong hai đường thẳng song song thì nó song song với đường thẳng kia
• C. Nếu một đường thẳng vuông góc với một trong hai đường thẳng song song thì nó tạo với đường thẳng một góc 60$^{\circ}$
• D. không có đáp án đúng

Câu 5: Chọn câu đúng.

• A. Giả thiết của định lý là điều cho biết;
• B. Kết luận của định lý là điều được suy ra;
• C. Giả thiết của định lý là điều được suy ra;

• D. Cả A, B đều đúng.

Câu 6: Điền vào chỗ chấm phần giả thiết để hoàn thành định lí sau:

Nếu hai đường thẳng phân biệt cùng … với một đường thẳng thứ ba thì chúng song song với nhau.

• A. Song song;

• B. Vuông góc;

• C. Cắt nhau;
• D. A, B, C đều đúng.

Câu 7: Trong các câu sau, câu nào cho một định lí

• A. Đường thẳng nào vuông góc với một trong hai đường thẳng song song thì vuông góc với đường thẳng kia

• B. Đường thẳng nào vuông góc với một trong hai đường thẳng cắt nhau thì song song với đường thẳng kia
• C. Nếu hai đường thẳng AB và AC cùng song song với một đường thẳng thứ ba thì hai đường thẳng đó song song
• D. Nếu hai đường thẳng cùng vuông góc với một đường thẳng thứ ba thì hai đường thẳng đó song song

Câu 8: Trong các câu sau, câu nào không cho một định lí

• A. Đường thẳng nào vuông góc với một trong hai đường thẳng song song thì vuông góc với đường thẳng kia
• B. Nếu một đường thẳng cắt hai đường thẳng song song thì tạo ra các cặp góc so le trong, cặp góc đồng vị bằng nhau
• C. Hai góc đối đỉnh thì bằng nhau

• D. Hai góc kề nhau có tổng số đo là 180$^{\circ}$

Câu 9:  Phát biểu bằng lời định lí sau:

• A. Hai góc cùng phụ một góc thứ ba thì bằng nhau;

• B. Hai góc cùng bù một góc thứ ba thì bằng nhau;
• C. Hai góc cùng phụ một góc thứ ba thì bù nhau;
• D. Hai góc cùng phụ một góc thứ ba thì kề nhau.

Câu 10: Hãy chỉ ra giải thiết của định lí sau: Nếu một đường thẳng cắt hai đường thẳng sao cho có một cặp góc so le trong bằng nhau thì hai đường thẳng đó song song.

• A. Một đường thẳng cắt hai đường thẳng sao cho có một cặp góc so le trong bằng nhau;

• B. Hai đường thẳng đó song song;
• C. Đáp án A và B đúng;
• D. Đáp án A và B sai.

Câu 11: Trong định lí “Hai góc đối đỉnh thì bằng nhau”. Giả thiết của định lí là:

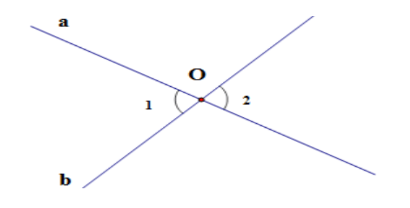
• A. a cắt b tại O;

• B. góc O1 và góc O2 là hai góc đối đỉnh;

• C. góc O1 và góc O2 là hai góc bằng nhau;
• D. góc O1 và góc O2 là hai góc nhọn.

Câu 12: Trong các câu sau,Câu nào cho một định lí:

• A. Góc tạo bởi hai tia phân giác của hai góc kề bù là một góc vuông;

• B. Góc tạo bởi hai tia phân giác của hai góc kề bù là một góc nhọn;
• C. Góc tạo bởi hai tia phân giác của hai góc kề bù là một góc bẹt;
• D. Góc tạo bởi hai tia phân giác của hai góc kề bù là một góc tù.

Câu 13: Chọn câu sai:

• A. Định lí thường được phát biểu ở dạng: "Vì ... nên ..."

• B. Giả thiết được viết tắt là GT, kết luận được viết tắt là KL
• C. Để chỉ ra một khẳng định không đúng, ta có thể chỉ ra một phản ví dụ
• D. Để chỉ ra một khẳng định đúng, ta đi chứng minh

Câu 14: Cho định lí: "Nếu hai đường thẳng song song cắt đường thẳng thứ ba thì hai góc đồng vị bằng nhau. Giả thiết của định lí là:

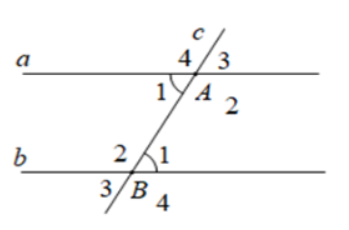
• A. $a//b; a\perp c$

• B. $a//b,c\cap a={A};c\cap b={B}$

• C. a//b; a//c
• D. a//b, c bất kì

Câu 15: Khi chứng minh một định lí, người ta cần:

• A. Chứng minh định lí đó đúng trong một trường hợp cụ thể của giả thiết;
• B. Chứng minh định lí đó đúng trong hai trường hợp cụ thể của giả thiết;

• C. Chứng minh định lí đó đúng trong mọi trường có thể xảy ra của giả thiết;

• D. Chứng minh định lí đó đúng trong vài trường hợp cụ thể của giả thiết.

Câu 16: Phát biểu bằng lời định lí sau:

• A. Nếu một đường thẳng cắt hai đường thẳng phân biệt thì chúng song song với nhau;
• B.Nếu hai đường thẳng phân biệt cùng vuông góc với đường thẳng thứ ba thì chúng vuông góc với nhau;

• C. Nếu hai đường thằng phân biệt cùng vuông góc với đường thẳng thứ ba thì chúng song song với nhau;

• D. Nếu hai đường thẳng phân biệt cùng vuông góc với đường thẳng thứ ba thì chúng cắt nhau.

Câu 17: Điền vào chỗ trống bằng những nội dung thích hợp để được các định lí: “Nếu M là trung điểm của đoạn thẳng AB thì …”

• A. M nằm giữa A và B;

• B. MA = MB;
• C. MA = MB = AB;
• D. MA + MB = AB.

Câu 18: Chọn khẳng định đúng trong những khẳng định sau đây.

• A. Chứng minh định lí là dùng lập luận để từ giả thiết suy ra kết luận;
• B. Định lí là một khẳng định được suy ra từ những khẳng định được coi là đúng;

• C. A, B đều đúng;

• D. A, B đều sai.

Câu 19: Trong định lí “Một đường thẳng vuông góc với một trong hai đường thẳng song song thì nó cũng vuông góc với đường thẳng còn lại”.

Giả thiết: a // b, a ⊥ c. Kết luận của định lí trên là:

• A. a // b, a ⊥c;
• B. a // b;

• C. b ⊥c;

• D. a // b, a ⊥c, b ⊥ c.

Câu 20: Cho định lí có giả thiết: góc xOy và x’Oy’ là hai góc đối đỉnh (như hình vẽ). Kết luận của định lí là:

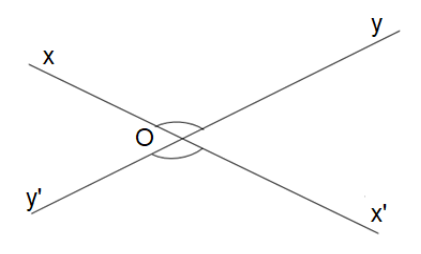
• A.$\widehat{xOy}=\widehat{x'Oy'}$
• B. $\widehat{xOy}=\widehat{x'Oy}$

• C. $\widehat{xOy}=\widehat{xOy'}$

• D. A, B đều đúng.