1.ĐƯỜNG CAO CỦA TAM GIÁC

HĐKP1:

=> Kết luận:

Đoạn thẳng vuông góc kẻ từ một đỉnh của một tamm giác đến đường thẳng chứa cạnh đối diện gọi là đường cao của tam giác đó.

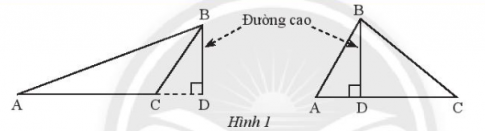
Ví dụ 1: SGK – tr 77

Chú ý: Mỗi tam giác có ba đường cao.

Thực hành 1: 

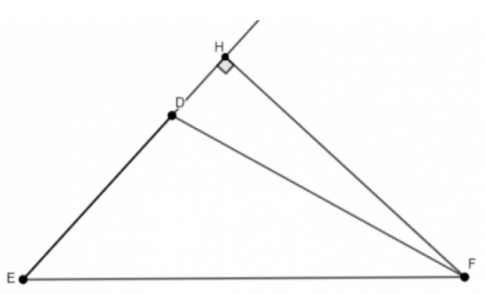
Vận dụng 1:

a) Đường cao từ đỉnh B của tam giác ABC là BA (vì BA ⊥ AC).

b) 

2. TÍNH CHẤT BA ĐƯỜNG CAO CỦA TAM GIÁC

HĐKP2:

Cả 3 đường cao đều cùng đi qua một điểm.

Định lí:

Ba đường cao của một tam giác cùng đi qua một điểm.

Chú ý:

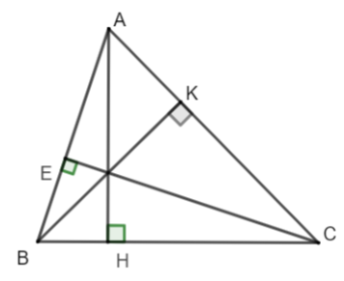
- Ta còn nói ba đường cao AD, BE, CF đồng quy tại H. Điểm H được gọi là trực tâm của tam giác ABC. 

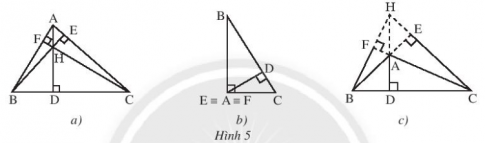
- Tam giác nhọn có trực tâm nằm bên trong tam giác.(H5.a)

- Tam giác vuông có trực tâm trùng với đỉnh góc vuông. (H.5b)

- Tam giác tù có trực tâ nằm ngoài tam giác. (H.5c)

Thực hành 2:

Trong tam giác MNL  có :

LP ⊥ MN => LP là đường cao của tam giác MNL.

MQ ⊥ LN => MQ là đường cao của tam giác MNL.

LP giao với MQ tại S 

=> S là trực tâm của tam giác MNL

Vì 3 đường cao của tam giác cắt nhau tại 1 điểm.

=> NS ⊥ LM.

Vận dụng 2:

+ Xét ∆ HBC có HD ⊥ BC

                         CE ⊥ BH

                         BF ⊥ CH

=> Tam giác HBC có 3 đường cao là HD, CE, BF.

Mà BF, DH, CE giao nhau tại A

=> A là trực tâm của ∆ HBC.

+ Xét ∆ HAB có HF ⊥ AB

                         AE ⊥ BH

                         BD ⊥ AH

=> Tam giác HAB có 3 đường cao là HF, AE, BD.

Mà BD, FH, AE giao nhau tại C

=> C là trực tâm của ∆ HAB.

+ Xét ∆ HAC có HE ⊥ AC

                          AF ⊥ CH

                         CD ⊥ AH

=> Tam giác HAC có 3 đường cao là HE, AF, CD.

AF, HE, CD giao nhau tại B

=> B là trực tâm của ∆ HAC.