BÀI TẬP CUỐI CHƯƠNG 8

PHẦN I. HỆ THỐNG BÀI TẬP, BÀI GIẢI CUỐI SGK

1. HỆ THỐNG BÀI TẬP CUỐI SGK

Bài 1: Cho tam giác ABC cân tại A... Hai đường cao BE và CF cắt nhau tại H.

a) Chứng minh rằng ∆ BEC = ∆ CFB.

b) Chứng minh rằng ∆ AHF = ∆ AHE.

c) Gọi I là trung điểm của BC. Chứng minh rằng ba điểm A, H, I thẳng hàng.

Bài 2: Cho tam giác ABC vuông tại A, vẽ đường cao AH. Trên tia đối của tia HA lấy điểm M sao cho H là trung điểm của AM.

a) Chứng minh tam giác ABM cân.

b) Chứng minh rằng ∆ ABC = ∆ MBC.

Bài 3: Cho tam giác ABC vuông tại A ( AB , AC), vẽ đường cao AH. Trên tia đối của HC lấy điểm D sao cho HD = DC.

a) Chứng minh AC = AD.

b) Chứng minh rằng =  

Bài 4: Cho tam giác vuông ABC vuông tại A (AB < AC). Trên cạnh BC lấy điểm N sao cho BA = BN. Kẻ BE ⊥ AN (E thuộc AN).

a) Chứng minh rằng BE là tia phân giác của góc ABN.

b) Kẻ đường cao AH của tam giác ABC. Gọi K là giao điểm của AH với BE. Chứng minh rằng NK // CA.

c) Đường thẳng BK cắt AC tại F. Gọi G là giao điểm của đường thẳng AB và NF. Chứng minh rằng tam giác GBC cân.

Bài 5: Cho tam giác ABC nhọn ( AB < AC), vẽ đường cao AH. Đường trung trực của cạnh BC cắt AC tại M, cắt BC tại N.

a) Chứng minh rằng =  

b) Kẻ MI ⊥ AH (I thuộc AH), gọi K là giao điểm của AH với bM. Chứng minh rằng I là trung điểm của AK.

Bài 6: Cho tam giác nhọn MNP. Các trung tuyến ME và NF cắt nhau tại G. Trên tia đối của tia FN lấy điểm D sao cho FN = FD.

a) Chứng minh rằng ∆ MFN = ∆ PFD.

b) Trên đoạn thẳng FD lấy điểm H sao cho F là trung điểm của HG. Gọi K là trung điểm của PD. Chứng minh rằng 3 điểm M, H, K thẳng hàng.

Bài 7: Cho tam giác ABC vuông tại A có  AB = 1/2 AC, AD là tia phân giác của  (D thuộc BC). Gọi E là trung điểm của AC.

a) Chứng minh rằng DE = DB.

b) AB cắt DE tại K. Chứng minh rằng tam giác DCK cân và B là trung điểm của đoạn thẳng AK.

c) AD cắt CK tại H. Chứng minh rằng AH ⊥ CK.

Bài 8: Ở hình 1, cho biết AE = AF và =  .Chứng minh rằng AH là đường trung trực của BC.

Bài 9: Cho tam giác ABC vuông tại A. Tia phân giác của góc C cắt AB tại M. Từ B kẻ BH vuông góc với đường thẳng CM (H thuộc CM). Trên tia đối của HC lấy điểm E sao cho HE = HM.

a) Chứng minh rằng tam giác MBE cân.

b) Chứng minh rằng =

c) Chứng minh rằng EB ⊥ BC.

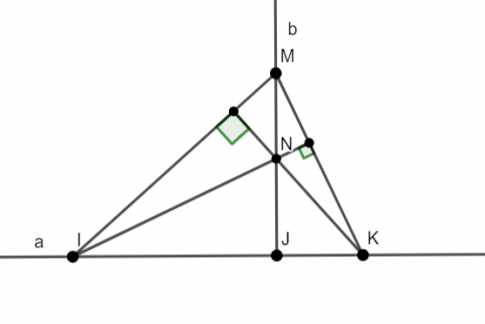
Bài 10:Trên đường thẳng a lấy 3 điểm phân biệt I, J, K (J ở giữa I và K). Kẻ đường thẳng b vuông góc với a tại J, trên b lấy điểm M khác điểm J. Đường thẳng qua I vuông góc với MK cắt b tại N. Chứng minh rằng KN vuông góc với MI.

2. 5 PHÚT GIẢI BÀI CUỐI SGK

Đáp án bài 1:

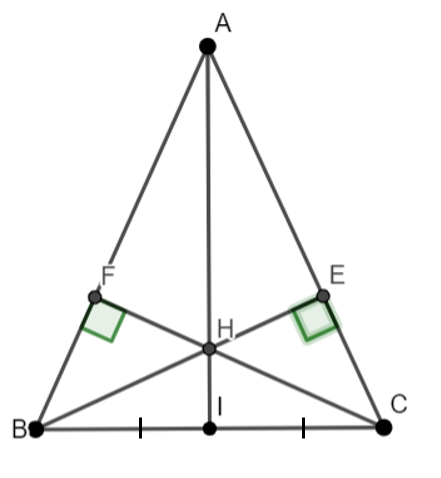
a) ∆ BEC = ∆ CFB (gn-cgv)

b) ∆ AFH = ∆ AEH (ch-cgv).

c)  AH ⊥ BC (1);  AI ⊥ BC (2). Từ (1) và (2) => A, I, H thẳng hàng. 

Đáp án bài 2: 

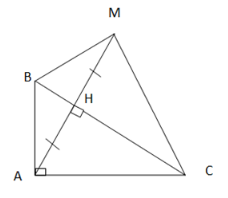
a) ∆BHA = ∆BHM (cgv-cgv) => BA = BM => ∆ABM cân tại B.

b) ∆ABC = ∆MBC (c.g.c)

Đáp án bài 3:

a) ∆AHD và ∆AHC (cgv-cgv) => AC = AD

b) CM = , mà ∆ ACD cân tại A =>   = =>  =   

Đáp án bài 4: 

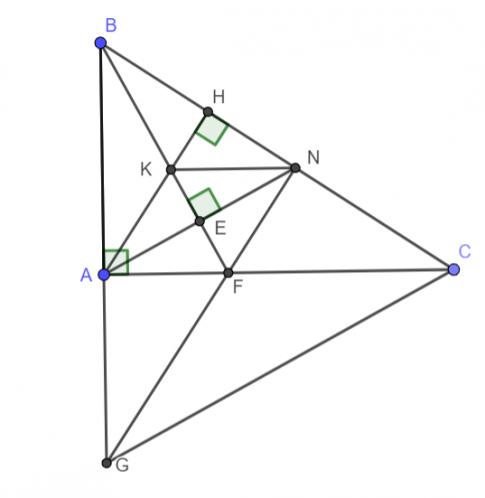
a) ∆ABE = ∆NBE (ch-cgv) = BE là tia phân giác của góc ABN.

b) NK ⊥ AB mà AC ⊥ AB NK // AC.

c) ∆MIK = ∆MIA (gn-cgv) => IK = IA => I là trung điểm của AK.

Đáp án bài 5: 

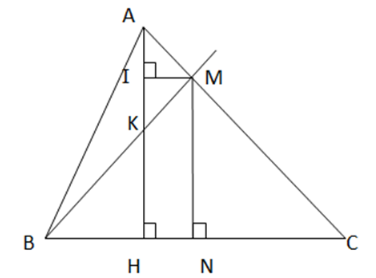
a) ∆ MBN  = ∆ MCN ( c.c.c) => =

∆ AHC vuông góc tại H =>  + = 90° (1)

∆ MNC vuông góc tại N =>  + = 90° =>  + = 90° (2)

Từ (1) và (2) ta có : =  

b)  ∆MIK = ∆MIA (gn-cgv) => IK = IA => I là trung điểm của AK.

Đáp án bài 6: 

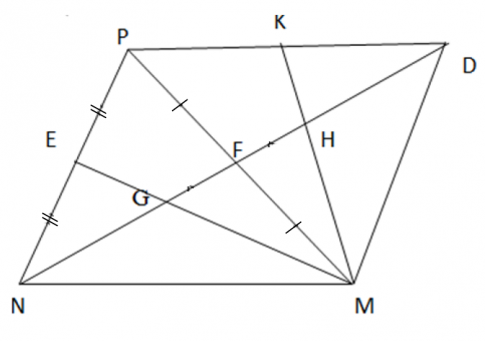
a)  ∆MFN = ∆PFD (c.g.c).

b) MH là đường trung tuyến của ∆PDM; MK là đường trung tuyến của ∆PDM M, H, K thẳng hàng.

Đáp án bài 7:

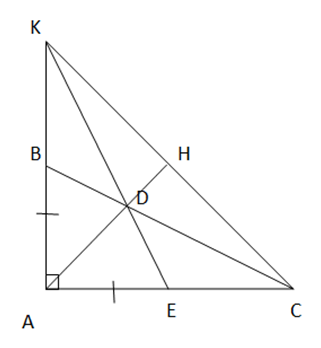
a) ∆ ABD =  ∆ AED (c.g.c) => BD = ED

b) +) =  ∆CDE =  ∆KDB (g.c.g) DC = DK ∆DCK cân tại D +) E là trung điểm của AC nên EC = AE = AC mà AB = AC KB = AB mà A, B, K thẳng hàng B là trung điểm của AK

c) ∆KAH =  ∆CAH (c.g.c) = , mà + = 180° => =  90° => AH ⊥ CK (đpcm) 

Đáp án bài 8: 

+) A thuộc đường trung trực của BC (1)

+) ∆FCB =  ∆EBC (c.g.c) =  ∆HCB cân tại H HC = HB 

H thuộc đường trung trực của BC (2)

Từ (1) và (2) AH là đường trung trực của BC.

Đáp án bài 9: 

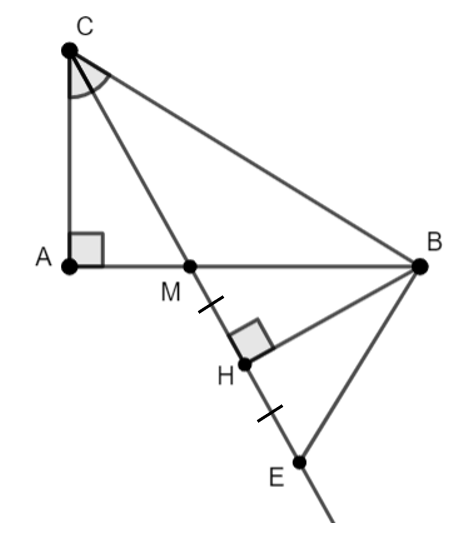
a)  ∆BHM =  ∆BHE (cgv-cgv)=> MB = BE => ∆MBE cân tại B

b)   = (=

c) 2 = ; 2 = => EB ⊥ BC.

Đáp án bài 10: MJ là đường cao của ∆ IMK; IN là đường cao của ∆IMK => N là trực tâm của ∆ IMK => KN ⊥ MI.