BÀI 6: TÍNH CHẤT BA ĐƯỜNG TRUNG TRỰC CỦA TAM GIÁC

1. ĐƯỜNG TRUNG TRỰC CỦA TAM GIÁC

Bài 1: Cho tam giác ABC, em hãy dùng thước kẻ và compa vẽ đường trung trực xy của cạnh BC

Giải rút gọn:

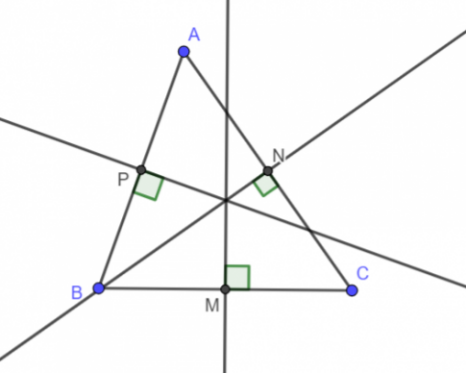
Bài 2: Cho tam giác nhọn ABC có M, N, P lần lượt là trung điểm của các cạnh BC, CA, AB. Vẽ ba đường trung trực của tam giác ABC. 

Giải rút gọn:

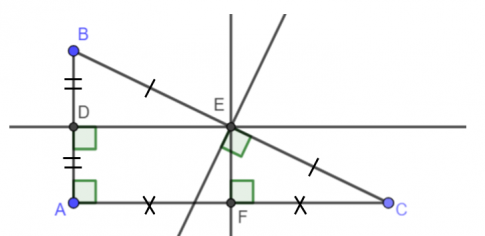
Bài 3: Vẽ ba đường trung trực của tam giác vuông ABC vuông tại A.

Giải rút gọn:

2. TÍNH CHẤT BA ĐƯỜNG TRUNG TRỰC CỦA TAM GIÁC

Bài 1: Gọi O là giao điểm của hai đường trung trực ứng với cạnh AB, AC của tam giác ABC (hình 2).

- Hãy so sánh độ dài 3 đoạn thẳng OA, OB, OC.

- Theo em, đường trung trực ứng với cạnh BC có đi qua điểm O hay không?

Giải rút gọn:

+) O thuộc đường trung trực của AB OA = OB

+) O thuộc đường trung trực của AC OA = OC

OA = OB = OC.

+) OB = OC đường trung trực của BC đi qua O .

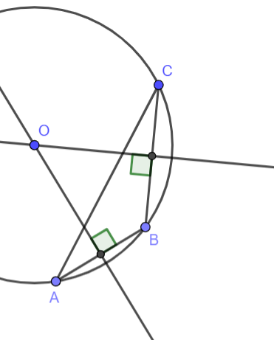
Bài 2: Gọi O là giao điểm của ba đường trung trực của tam giác ABC ( Hình 4 ). Hãy dùng compa vẽ đường tròn tâm O bán kính OA và cho biết đường tròn này có đi qua 2 điểm B và C hay không.

Giải rút gọn:

O là giao điểm của ba đường trung trực OA = OB = OC

đường tròn tâm O bán kính OA có đi qua B, C.

Bài 3: Trên bản đồ quy hoạch một khu dân cư có ba điểm dân cư A, B, C ( Hình 5). Tìm địa điểm M để xây một trường học sao cho trường học này cách đều ba điểm dân cư đó.

Giải rút gọn:

M là giao của ba đường trung trực của ΔCAB.

BÀI TẬP CUỐI SGK

Bài 1:Vẽ ba tam giác nhọn, vuông, tù

a) Xác định điểm O cách đều 3 đỉnh của mỗi tam giác.

b) Nêu nhận xét của em về vị trí điểm O trong mỗi trường hợp.

Giải rút gọn:

a) 

b) 

+) Δ nhọn: O nằm trong ΔABC.

+) Δ tù: O nằm ngoài ΔABC.

     +) Δvuông: điểm O nằm trên cạnh huyền BC.

Bài 2: Cho tam giác nhọn ABC. Gọi M, N, P lần lượt là trung điểm của các cạnh AB, BC, CA và cho O là điểm cách đều ba đỉnh của tam giác ABC. Chứng minh rằng MO vuông góc với AB, NO vuông góc với BC và PO vuông góc với AC.

Giải rút gọn:

+) AM = MB, OA = OB , chung MO => ∆AOM = ∆BOM (c.c.c)

=  Mà  + = 180° => = = 90°

OM ⊥ AB

+) Chứng minh tương tự ta có :  ON ⊥ BC; OP ⊥ AC.

Bài 3: Người ta muốn phục chế lại đĩa cổ hình tròn bị vỡ chỉ còn lại một mảnh (hình 6). Làm thế nào để xác định bán kính bị vỡ của đĩa cổ này?

Giải rút gọn: 

+) Lấy 3 điểm A, B, C bất kì thuộc cung tròn.

+) 2 đường trung trực của cạnh AB và BC cắt nhau tại O

OA = OB = OC là bán kính của đĩa.