BÀI 13: TÍNH CHẤT BA ĐƯỜNG CAO CỦA TAM GIÁC

Khởi động

Câu hỏi: Cho tam giác ABC. Gọi M, N, P lần lượt là hình chiếu của A, B, C trên các đường thẳng BC, CA, AB. Em có nhận xét gì về ba đường thẳng AM, BN, CP.

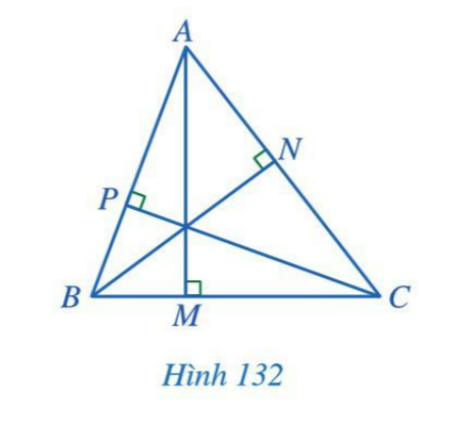
Giải rút gọn:

AM, BN, CP cùng đi qua trực tâm của △ABC.

I. Đường cao của tam giác

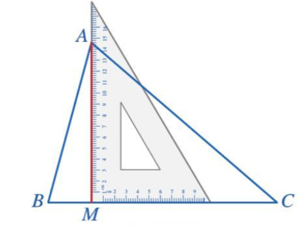
Bài 1: Cho tam giác ABC (Hình 133). Bằng cách sử dụng ê ke, vẽ hình chiếu M của điểm A trên đường thẳng BC.

Giải rút gọn:

Bài 2: Cho tam giác ABC vuông tại A. Hãy đọc tên đường cao đi qua B, đường cao đi qua C

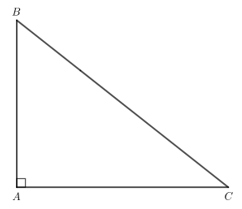
Giải rút gọn:

Đường cao đi qua B và ⊥AC là AB.

Đường cao đi qua C và ⊥AB là AC.

II. Tính chất ba đường cao của tam giác

Bài 1: Quan sát ba đường cao AM, BN, CP của tam giác ABC cho biết 3 đường cao đó có cùng đi qua 1 điểm hay không?

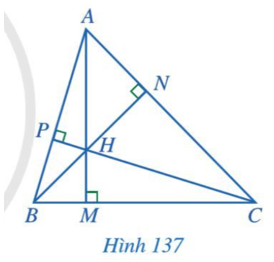
Giải rút gọn:

AM, BN, CP có cùng đi qua điểm H.

Bài 2: Cho tam giác đều ABC có trọng tâm là G. Chứng minh G cũng là trực tâm của tam giác ABC.

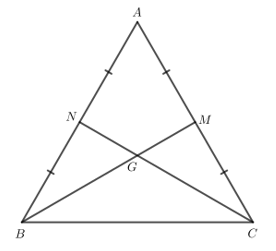
Giải rút gọn:

Gọi M, N là trung điểm của AC và AB.

Ta có: △ABC đều => AB = BC = CA và .

Mà M là trung điểm của AC => AM = CM.

Xét ∆BAM và ∆BCM có:

BA = BC (cmt); ; AM = CM (cmt).

=> ∆BAM = ∆BCM (c.g.c).

=> (góc tương ứng).

Mà =>

Do đó BM là đường cao của △ABC.

Tương tự CN là đường cao của △ABC. 

Mà BM ∩ CN = G => G là trực tâm của △ABC.

Bài 3: Cho tam giác ABC có trực tâm H cũng là trọng tâm của tam giác. Chứng minh tam giác ABC đều.

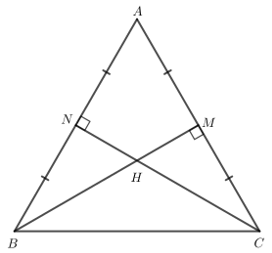
Giải rút gọn:

Gọi M, N lần lượt là trung điểm của AC và AB.

Do H là trực tâm của △ABC nên CH ⊥ AB, BH ⊥ AC hay CN ⊥ AB, BM ⊥ AC.

Lại có H là trọng tâm của △ABC nên BM, CN là các đường trung tuyến của △ABC.

BM ⊥ AC tại trung điểm M của AC => BM là đường trung trực của AC.

=> BA = BC 

Do CN ⊥AB tại trung điểm N của AB => CN là đường trung trực của AB.

=> CA = CB 

=> AB = BC = CA nên △ABC đều.

III. Bài tập

Bài 1: Tam giác ABC có H là trực tâm, H không trùng với đỉnh nào của tam giác. Nêu một tính chất của cặp đường thẳng

a. AH và BC

b. BH và CA

c. CH và AB

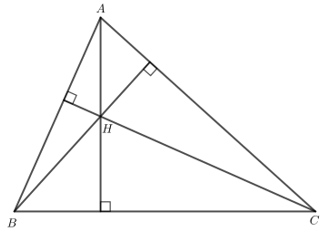
Giải rút gọn:

a) AH ⊥ BC.

b) BH ⊥ CA.

c) CH ⊥ AB.

Bài 2: Cho tam giác ABC. Vẽ trực tâm H của tam giác ABC và nhận xét vị trí của nó trong các trường hợp sau:

a. Tam giác ABC nhọn

b. Tam giác ABC vuông tại A

c. Tam giác ABC có góc A tù

Giải rút gọn:

a) 

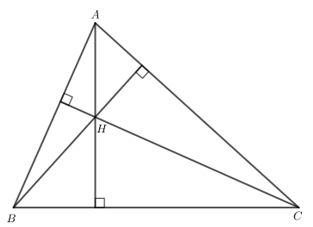
Nhận xét: H nằm trong △ABC.

b) 

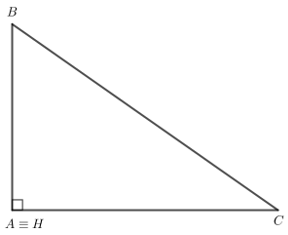
Nhận xét: A trùng H.

c) 

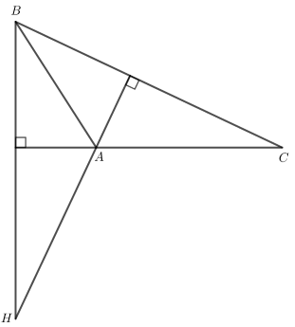
Nhận xét: H nằm ngoài △ABC.

Bài 3: Cho tam giác nhọn ABC và điểm D nằm trong tam giác. Chứng minh rằng nếu DA vuông góc với BC và DB vuông góc với CA thì DC vuông góc với AB.

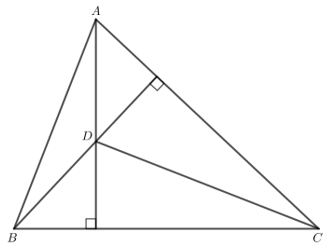
Giải rút gọn:

△ABC có: DA ⊥ BC, DB ⊥ CA.

Mà DA ∩ DB = D => D là trực tâm của △ABC => DC ⊥ AB.

Bài 4: Cho tam giác nhọn ABC. Hai đường cao BE và CF cắt nhau tại H, = 25^°. Tính và

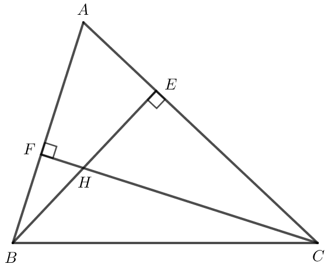
Giải rút gọn:

Xét ∆AFC vuông tại F có: 

=> hay

Xét ∆BEA vuông tại E có: 

=> hay .

Bài 5: Trong Hình 139, cho biết AB // CD, AD // BC; H, K lần lượt là trực tâm các tam giác ABC và ACD. Chứng minh AK // CH và AH // CK.

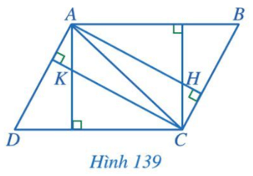
Giải rút gọn:

Ta có:

+) CH ⊥ AB và AH ⊥ BC (H là trực tâm của △ABC) 

+) AK ⊥ CD và CK ⊥ AD (K là trực tâm của △ADC)

Do AB // CD nên AK ⊥ AB mà CH ⊥ AB => AK // CH.

Do AD // BC nên AH ⊥ AD mà CK ⊥ AD => AH // CK.

Bài 6: Cho tam giác ABC có G là trọng tâm, H là trực tâm, I là giao điểm của ba đường phân giác, O là giao điểm của ba đường trung trực. Chứng minh rằng:

a) Nếu tam giác ABC đều thì bốn điểm G, H, I, O trùng nhau;

b) Nếu tam giác ABC có hai điểm H, I trùng nhau thì tam giác ABC là tam giác đều.

Giải rút gọn:

a) 

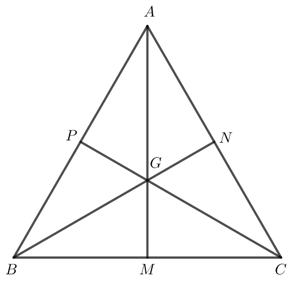
Gọi M, N, P lần lượt là trung điểm của BC, CA, AB.

Ta có: △ABC đều => AB = BC = CA và

Do M là trung điểm của BC nên BM = CM.

Xét ∆AMB và ∆AMC có:

AB = AC (cmt); ; BM = CM (cmt).

=> ∆AMB = ∆AMC (c.g.c).

=> và (góc tương ứng).

Do  mà nên .

Khi đó AM ⊥ BC tại trung điểm M của BC nên AM là đường trung trực của BC.

Lại có nên Am là đường phân giác của .

Chứng minh tương tự: 

+ BN là đường trung trực của CA và BN là đường phân giác của .

+ CP là đường trung trực của AB và CP là đường phân giác của .

Mà AM, BN, CP cắt nhau tại G nên G, H, I, O trùng nhau.

b) 

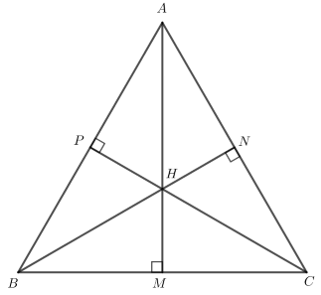
Gọi M, N, P lần lượt là chân đường cao kẻ từ H đến BC, CA, AB.

Khi đó HN ⊥ AC mà H là trực tâm của ∆ABC => BH ⊥ AC.

HN ⊥ AC, BH ⊥ AC nên B, H, N thẳng hàng.

+ Xét ∆APH vuông tại P và ∆CMH vuông tại M có:

; HP = HM (gt).

=> ∆APH = ∆CMH (góc nhọn - cạnh góc vuông).

=> HA = HC (cạnh tương ứng).

+ Xét ∆HNA và ∆HNC cùng vuông tại N có:

HN chung; HA = HC (cmt).

=> ∆HNA = ∆HNC (2 cạnh góc vuông).

=> AN = CN (cạnh tương ứng).

Khi đó N là trung điểm của AC.

HN ⊥ AC tại trung điểm N của AC nên HN là đường trung trực của AC.

Mà B, H, N thẳng hàng nên B thuộc đường trung trực của AC.

Do đó BA = BC.

Thực hiện tương tự, ta chứng minh được CA = CB.

Do đó AB = BC = CA => △ABC đều.