BÀI 10: TÍNH CHẤT BA ĐƯỜNG TRUNG TUYẾN CỦA TAM GIÁC

Khởi động

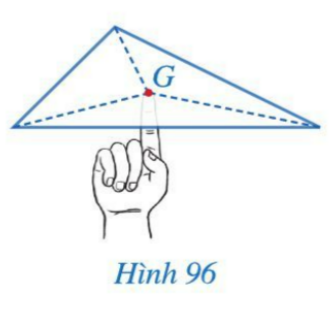
Câu hỏi: Hình 96 minh họa một miếng bìa phẳng có dạng hình tam giác đặt thăng bằng trên đầu ngón tay tại điểm G. Điểm được xác định như thế nào?

Giải rút gọn:

Điểm G được xác định bằng cách: lấy giao điểm của ba đường trung tuyến của tam giác.

I. Đường trung tuyến của tam giác

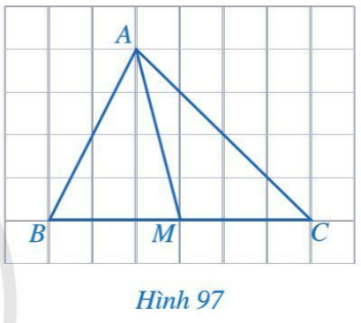
Bài 1: Quan sát hình 97 và cho biết các đầu mút của đoạn thẳng AM có đặc điểm gì?

Giải rút gọn:

Đầu mút A là một đỉnh của △ABC, đầu mút M là trung điểm của cạnh BC.

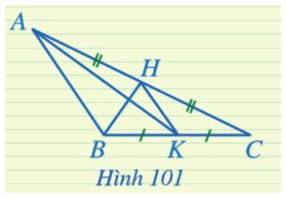
Bài 2: Trong hình 101, đoạn HK là đường trung tuyến của những tam giác nào?

Giải rút gọn:

HK là đường trung tuyến của △AKC và △BHC

II. Tính chất ba đường trung tuyến của tam giác

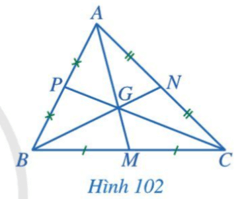
Bài 1: Quan sát các đường trung tuyến AM, BN, CP của tam giác ABC trong Hình 102, cho biết ba đường trung tuyến đó có cùng đi qua một điểm hay không?

Giải rút gọn:

Ta thấy ba đường trung tuyến cùng đi qua điểm G.

Bài 2: Cho tam giác PQR có hai đường trung tuyến QM và RK cắt nhau tại G. Gọi I là trung điểm của cạnh QR. Chứng minh rằng 3 điểm P, G, I thằng hàng

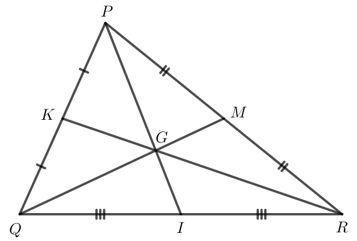
Giải rút gọn:

△PQR có: QM ∩ RK = G

=> G là trọng tâm của △PQR

Mà I là trung điểm của cạnh QR (gt) => PI là đường trung tuyến của △PQR.

=> P, G, I thẳng hàng.

Bài 3: Quan sát các đường trung tuyến AM, BN, CP của tam giác ABC trong hình 104. Bằng cách đếm số ô vuông, tìm các tỉ số ...

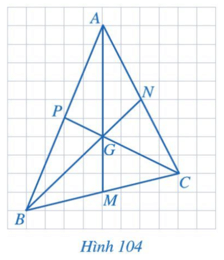
Giải rút gọn:

III. Bài tập

Bài 1: Cho tam giác ABC. Ba đường trung tuyến AM, BN, CP đồng quy tại G. Chứng minh: GA + GA + GC = (AM + BN + CP)

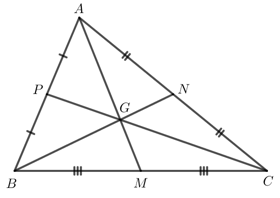
Giải rút gọn:

Xét △ABC có: G là trọng tâm của △ABC (AM, BN, CP đồng quy tại G)

=> .

Do đó (đpcm)

Bài 2: Cho tam giác ABC cân tại A, hai đường trung tuyến BM và CN cắt nhau tại G. Chứng minh:

a. BM = CN

b. ΔGBC cân tại G

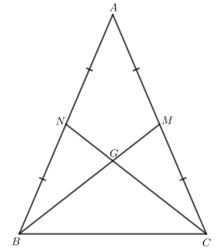
Giải rút gọn:

a) Xét △ABC cân tại A, có: 

+) AB = AC và

+) M, N lần lượt là trung điểm của AC và AB (BM và CN là hai đường trung tuyến)

=>  BN = MC (= AB)

Xét ∆NBC và ∆MCB có:

BN = MC (cmt); (cmt); BC chung.

=> ∆NBC = ∆MCB (c - g - c).

=> BM = CN (cạnh tương ứng).

b) △ABC có: G là trọng tâm của tam giác ABC (BM ∩ CN = G)

=>

Mà BM = CN nên GB = GC.

Xét △GBC có: GB = GC 

=> △GBC cân tại G.

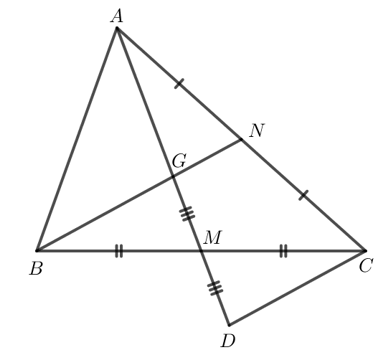
Bài 3: Cho tam giác ABC có hai đường trung tuyến AM và BN cắt nhau tại G. Trên tia đối của tia MA lấy điểm D sao cho MD = MG. Chứng minh:

a. GA = GD

b. ΔMBG = ΔMCD

c. CD = 2GN

Giải rút gọn:

a) △ABC có: G là trọng tâm (AM ∩ BN = G)

=>

Trên tia đối của tia MA lấy điểm D sao cho MD = MG nên M là trung điểm của GD =>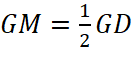

=> GA = GD 

b) Do M là trung điểm của GD nên MG = MD.

Xét ∆MBG và ∆MCD có:

MB = MC (gt); MG = MD (cmt)

(2 góc đối đỉnh)

=> ∆MBG = ∆MCD (c - g - c) => CD = BG (cạnh tương ứng).

c) Ta có: G là trọng tâm của △ABC => BG = 2GN.

Mà CD = BG (cmt) nên CD = 2GN.

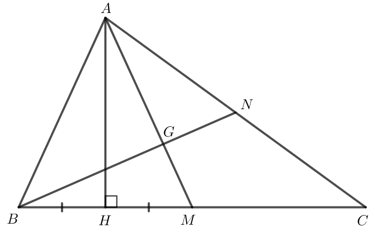
Bài 4: Cho tam giác ABC có hai đường trung tuyến AM và BN cắt nhau tại G. Gọi H là hình chiếu của A lên đường thẳng BC. Giả sử H là trung điểm của đoạn thẳng BM. Chứng minh: 

a. ΔAHB = ΔAHM

b. AG = AB

Giải rút gọn:

a) Do H là hình chiếu của A trên BC nên AH ⊥ BC.

Xét ∆AHB và ∆AHM đều vuông tại H có:

AH chung; HB = HM (gt).

=> ∆AHB = ∆AHM (2 cạnh góc vuông) => AB = AM (cạnh tương ứng).

b) Ta có: G là trọng tâm của ∆ABC (AM ∩ BN = G)

=>

Mà AB = AM (cmt) nên .

Bài 5: Hình 107 là mặt cắt đứng của một ngôi nhà ba tầng có mái dốc. Mỗi tầng cao 3,3 m. Mặt cắt mái nhà có dạng tam giác ABC cân tại A với đường trung tuyến AH dài 1,2 m. Tại vị trí O là trọng tâm tam giác ABC, người ta làm tâm cho một cửa sổ có dạng hình tròn.

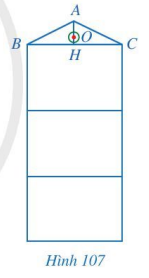
a) AH có vuông góc với BC không? Vì sao?

b) Vị trí O ở độ cao bao nhiêu mét so với mặt đất.

Giải rút gọn:

a) Xét ∆ABC cân tại A, có:

+) AB = AC và

+) H là trung điểm của BC (AH là đường trung tuyến của ∆ABC) 

=> BH = CH

Xét ∆ABH và ∆ACH có:

AB = AC (cmt); (cmt)

BH = CH (cmt).

=> ∆ABH = ∆ACH (c - g - c).

=> (góc tương ứng)

Mà nên hay AH ⊥ BC (đpcm)

b) Do O là trọng tâm của △ABC 

=> .

Do mỗi tầng cao 3,3 m nên vị trí O ở độ cao 0,4 + 3,3 . 3 = 10,3 m so với mặt đất.