BÀI 3: HAI TAM GIÁC BẰNG NHAU

Khởi động

Câu hỏi: Một dây chuyền sản xuất ra các sản phẩm có dạng hình tam giác giống hệt nhau (Hình 27). Khi đóng gói hàng, người ta xếp chúng chồng khít lên nhau. Khi hai tam giác có thể chồng khít lên nhau thì các cạnh và các góc tương ứng liên hệ với nhau như thế nào?

Giải rút gọn:

Thì các cạnh và các góc tương ứng sẽ bằng nhau.

I. Hai tam giác bằng nhau

Bài 1: Quan sát hai tam giác ABC và A’B’C’ trên một tờ giấy kẻ ô vuông (Hình 30).

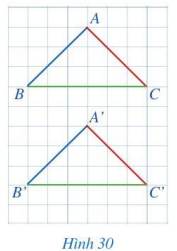
a) So sánh:

-        Các cặp cạnh: AB và A’B’; BC và B’C’; CA và C’A’.

-        Các cặp góc: A và A’; B và B’; C và C’.

b) Hai tam giác ABC và A’B’C’ có bằng nhau hay không?

c) Cắt mảnh giấy hình tam giác ABC và mảnh giất hình tam giác A’B’C’, hai hình tam giác đó có thể đặt chồng khít lên nhau hay không?

Giải rút gọn:

a) AB = A'B'; BC = B'C'; CA = C'A'

= ; = ; =

b) △ABC = △A'B'C.

c) Có vì hai tam giác bằng nhau.
Bài 2: Cho biết ΔABC = ΔMNP, AC = 4cm, =45⁰. Tín độ dài cạnh MP và số đo góc ACB

Giải rút gọn:

Ta có: ΔABC = ΔMNP

=> MP = AC = 4cm (cạnh tương ứng)

=> == 45⁰ (góc tương ứng)

II. Bài tập

Bài 1: Cho biết ΔABC = ΔDEG, AB=3cm, BC=4cm. CA=6cm. Tìm độ dài các cạnh của tam giác DEG

Giải rút gọn:

Ta có: ΔABC = ΔDEG (gt)

=> AB = DE = 3cm;  BC = EG = 4cm;  AC = DG = 6cm (các cặp cạnh tương ứng)

Bài 2: Cho biết ΔPQR = ΔIHK, = 71⁰, = 49⁰. Tính số đo góc K của tam giác IHK.

Giải rút gọn:

Xét ΔPQR có:

Mà ΔPQR = ΔIHK (gt) (góc tương ứng)

Bài 3: Cho ΔABC = ΔMNP, . Tính số đo góc P

Giải rút gọn:

Ta có (gt) mà (do ΔABC = ΔMNP)

Xét ΔMNP có: 

Bài 4: Cho tam giác ABC và điểm M thuộc cạnh BC thỏa mãn ΔAMB = ΔAMC (hình 32). Chứng minh rằng:

a. M là trung điểm của đoạn thẳng BC

b. Tia AM là tia phân giác của góc BA.

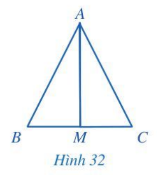
Giải rút gọn:

a. Ta có: ΔAMB = ΔAMC (gt)

=> BM = BC (cạnh tương ứng) 

=> M là trung điểm của BC.

b. Ta có: ΔAMB = ΔAMC (gt)

(góc tương ứng)

=> AM là tia phân giác của góc BAC 

Xét ΔABC có:

AM là đường trung tuyến (M là trung điểm của BC)

AM là tia phân giác của góc BAC (cmt)

=> AM là trung trực của ΔABC

=>