BÀI 4: TRƯỜNG HỢP BẰNG NHAU THỨ NHẤT CỦA TAM GIÁC: CẠNH – CẠNH – CẠNH

Khởi động

Câu hỏi: Giá để đồ ở hình 33 gợi lên hình ảnh tam giác ABC và A'B'C' có: AB=A'B'; BC=B'C'; CA=C'A'. Tam giác ABC có bằng tam giác A'B'C' hay không?

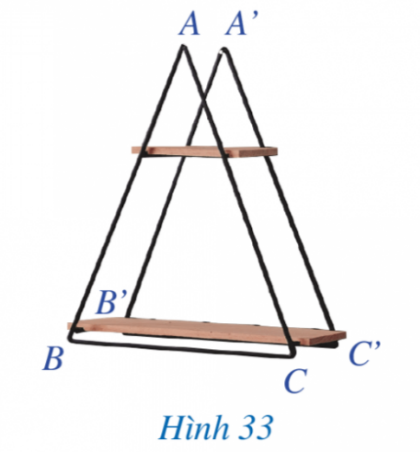
Giải rút gọn:

△ABC = △A'B'C'

I. Trường hợp bằng nhau cạnh – cạnh – cạnh (c.c.c)

Bài 1: Hai tam giác ở hình 37 có bằng nhau không? Vì sao?

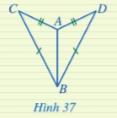
Giải rút gọn:

Xét △ABC và △ABD, có: 

AC = CD, BC = BD, AB chung 

=> ΔABC = ΔABD (c.c.c)

II. Áp dụng vào trường hợp bằng nhau về cạnh huyền và cạnh góc vuông của tam giác vuông 

Bài 1: Cho hai tam giác vuông ABC và A'B'C' có: ==90⁰, AB=A'B'=3cm, BC=B'C'=5cm. So sánh độ dài các cạnh AC và A'C'

Giải rút gọn:

Xét △ABC vuông tại A, có:

BC² = AB² + AC² (Định lý Pythagore)

=> AC = 4cm

Tương tự  △A'B'C' => A'C' = 4 cm

=> AC = A’C’

III. Bài tập

Bài 1: Cho Hình 42 có MN=QN; MP=QP. Chứng minh =

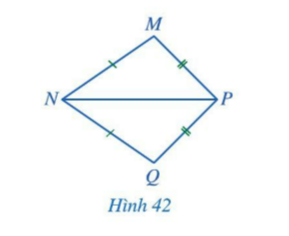
Giải rút gọn:

Xét △MNP và △NPQ, có:

MN = QN; MP = QP; NP chung

=> ΔMNP = ΔQNP (c.c.c)

=> = (góc tương ứng)

Bài 2: Cho Hình 43 có AB = AD, = 90⁰. Chứng minh

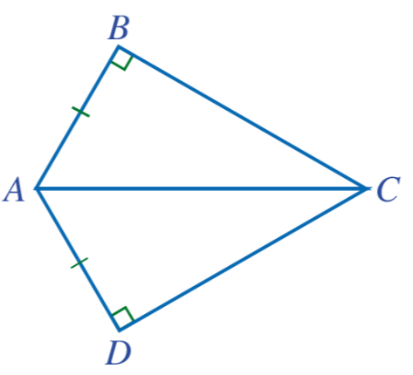
Giải rút gọn:

Xét △ABC và △ADC, có: 

= 90⁰

AB = AD (gt), AC là cạnh chung

=> ΔABC = ΔADC (cạnh huyền – cạnh góc vuông)

=> (góc tương ứng)

Bài 3: Cho hình 44 có AC = BD, = 90⁰. Chứng minh AD = BC.

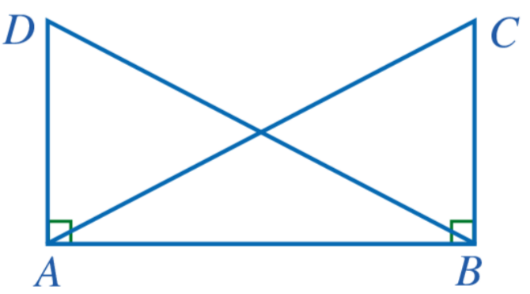
Giải rút gọn:

Xét ΔABC và ΔBAD, có: 

= 90⁰

AC = BD (gt), AB là cạnh chung

=> ΔABC = ΔBAD (cạnh huyền – cạnh góc vuông)

=> AD = BC (cạnh tương ứng)

Bài 4: Cho hai tam giác ABC và MNP thỏa mãn: AB = MN, BC = NP, AC = MP, , . Tính số đo các góc còn lại của hai tam giác.

Giải rút gọn:

Xét ΔABC và ΔMNP, có: 

AB = MN, BC = NP, AC = MP

=> ΔABC = ΔMNP (c.c.c)

;