Câu 1: Cho tam giác ABC có AB < AC. Gọi E $\in $ AC sao cho AB = CE. Gọi O là một điểm nằm ở trong tam giác sao cho OA = OC, OB = OE. KHi đó:

• A. ∆AOB = ∆CEO

• B. ∆AOB = ∆COE

• C. $\widehat{AOB}=\widehat{OEC}$
• D. $\widehat{ABO}=\widehat{OCE}$

Câu 2: Cho tam giác ABD và tam giác IKH có: AB = KI, AD = KH, DB = IH

Phát biểu nào trong các phát biểu sau đây là đúng:

• A. ∆BAD = ∆HIK
• B. ∆ABD = ∆KHI
• C. ∆DAB = ∆HIK

• D. ∆ABD=∆KIH

Câu 3: Cho hình vẽ dưới đây. Khẳng định đúng là

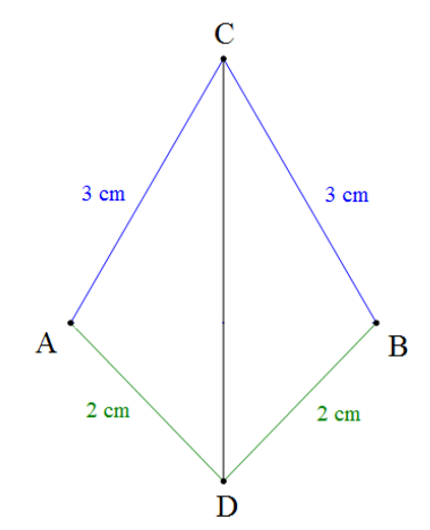
• A. $\widehat{DAC}=\widehat{ADB}$
• B. $\widehat{DAC}=\widehat{ACB}$

• C. $\widehat{DAC}=\widehat{DBC}$

• D. $\widehat{DAC}=\widehat{BDC}$

Câu 4: Cho tam giác MNP có MN = MP. Gọi A là trung điểm của NP. BIết $\widehat{NMP}=40°$ thì số đo góc MPN là:

• A. 100°

• B. 70°

• C. 80°
• D. 90°

Câu 5: Cho hình vẽ sau. Tam giác bằng tam giác ABD là

• A. ∆ABC;
• B. ∆AED;

• C. ∆AEC;

• D. ∆ACD.

Câu 6: Cho hình vẽ dưới đây, biết JG = JL, GK = LK, $\widehat{KJL}=60°,\widehat{JGK}=90°$. Số đo góc GKL là

• A. 90°;
• B. 30°;

• C. 60°;

• D. 120°.

Câu 7: Cho tam giác ABC có AB = AC và MB = MC ($M\in BC$). Chọn câu sai

• A. ∆AMC = ∆BCM

• B. ∆AMB = ∆AMC
• C. $AM\perp BC$
• D $\widehat{BAM}=\widehat{CAM}$

Câu 8: Cho ∆ABC có AC > AB. Trên cạnh AC lấy điểm E sao cho CE = AB. Gọi O là một điểm sao cho OA = OC và OB = OE (hình vẽ). So sánh góc OAB và góc OCA đúng là

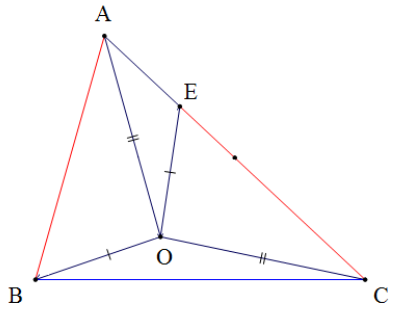
• A. $\widehat{OAB}=\widehat{OCA}$

• B. $\widehat{OAB}>\widehat{OCA}$
• C. $\widehat{OAB}<\widehat{OCA}$
• D. Khong đủ dữ kiện để so sánh

Câu 9: Cho $\widehat{xOy}$ khác góc bẹt, lấy điểm A thuộc tia Ox, điểm B thuộc tia Oy sao cho OA = OB. Lấy M là trung điểm của AB. Khẳng định nào dưới đây đúng?

• A. ∆OBM = ∆OMA;
• B. $\widehat{OMB}=\widehat{OAM}$
• C. ∆OBM = ∆OBA;

• D. OM là tia phân giác của góc 

Câu 10: Cho tam giác AMN có AM = AN và  là trung điểm MN. Chọn câu đúng nhất

• A. $\widehat{AMI}=\widehat{ANI}$
• B. $AI\perp MN$
• C. ∆AIM = ∆AIN

• D. Cả A, B, C đều đúng

Câu 11: Cho tam giác ABD và tam giác IKH có: AB = KI, AD = KH, DB = IH. Nếu $\widehat{A}=60°$, thì số đo góc K là

• A. 60°

• B. 70
• C. 90°
• D. 120°

Câu 12: Cho hình dưới đây

Chọn câu sai.

• A. AD // BC
• B. AB // CD
• C. ∆ ABC = ∆CDA

• D. ∆ABC = ∆ADC

Câu 13: Cho hai tam giác ABD và CDB có cạnh chung BD. Biết AB = DC và AD = CB. Phát biểu nòa sau đây là sai

• A. ∆ABC = ∆CDA
• B. $\widehat{ABC}=\widehat{CDA}$

• C. $\widehat{BAC}=\widehat{DAC}$

• D. $\widehat{BCA}=\widehat{DAC}$

Câu 14: Cho hình vẽ dưới đây. Khẳng định đúng là

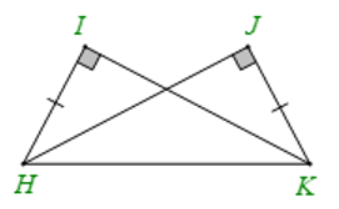
• A. ∆HIK = ∆HJK
• B. ∆HIK = ∆JHK
• C. ∆HIK = ∆KHJ

• D. ∆HIK = ∆KJH

Câu 15: Trên đường thẳng xy lấy hai điểm A, B. Trên cùng nửa mặt phẳng bờ xy lấy hai điểm C và C' sao cho AC = BC'; BC = AC'. Chọn câu đúng.

• A. $\widehat{BCA}=\widehat{BAC'}$
• B. $\widehat{BCA}=\widehat{ABC'}$
• C. ∆ACB = ∆BAC'

• D. ∆ACB = ∆BC'A

Câu 16: Cho đoạn thẳng AB = 6 cm. Trên một nửa mặt phẳng bờ AB vẽ tam giác ABC sao cho AC = 4 cm, BC = 5 cm, trên nửa mặt phẳng còn lại vẽ tam giác ABD sao cho BD = 4 cm, AD = 5 cm. Chọn câu đúng

• A. ∆CAB = ∆BAD
• B. ∆ABC = ∆BDA

• C. ∆CAB = ∆DBA

• D. ∆CAB = ∆ABD

Câu 17: Cho hình vẽ dưới đây, biết AB = CD; AD = BC. Góc có số đo bằng góc ABC là

• A. $\widehat{DAC}$
• B. $\widehat{ACB}$
• C. $\widehat{ACD}$

• D. $\widehat{CDA}$

Câu 18: Trên đường thẳng xy lấy hai điểm A, B. Trên cùng nửa mặt phẳng bờ xy lấy hai điểm C và C' sao cho AC = BC'; BC = AC'. So sánh hai góc $\widehat{CAC'};\widehat{CBC'}$

• A. $\widehat{CAC'}>\widehat{CBC'}$
• B. $\widehat{CAC'}<\widehat{CBC'}$

• C. $\widehat{CAC'}=\widehat{CBC'}$

• D. $\widehat{CAC'}=2\widehat{CBC'}$

Câu 19: Cho đoạn thẳng BC = 10 cm. Trên một nửa mặt phẳng bờ BC vẽ tam giác ABC sao cho AC = 6 cm, BC = 8 cm, trên nửa mặt phẳng còn lại vẽ tam giác DBC sao cho BD = 6 cm, AC =8 cm. Chọn câu đúng

• A. ∆CAB = ∆BCD
• B. ∆ABC = ∆BCD

• C. ∆CAB = ∆CBD

• D. ∆CAB = ∆DBC

Câu 20: Cho $\widehat{xOy}=50°$, vẽ cung tròn tâm O bán kính 2 cm, cung tròn này cắt Õ, Oy lần lượt tại S, B. Vẽ các cung tròn tâm A và B có bán kính 3 cm, chúng cắt nhau tại điểm C nằm trong góc xOy. Tính $\widehat{xOC}$

• A. 25°

• B. 50°
• C. 80°
• D. 90°