Câu 1: Cho ∆ABC có ba góc nhọn (AB < AC), đường cao AH. Lấy D là điểm thuộc đoạn HC, vẽ DE ⊥ AC (E ∈ AC). Gọi K là giao điểm của AH và DE. Khẳng định nào sau đây đúng?

• A. AD // KC;
• B. AD trùng KC;
• C. AD cắt KC nhưng không vuông góc với KC;

• D. AD ⊥ KC.

Câu 2: Cho ∆MNO, hai đường cao NF và ME cắt nhau tại H. Phát biểu đúng là

• A. OH là đường phân giác của ∆MNO;
• B. OH là đường trung trực của cạnh MN;
• C. OH là đường trung tuyến của ∆MNO;

• D. OH là đường cao của ∆MNO.

Câu 3: Cho tam giác nhọn MNP có hai đường cao NE và PF cắt nhau tại H. Biết NE = PF. Khẳng định đúng là

• A. ∆MNP cân tại N;
• B. ∆MEF cân tại E;
• C. H là trọng tâm ∆MNP;

• D. MH ⊥ BC.

Câu 4: Cho ∆ABC cân tại A có $\widehat{A}$ = 45°. Kẻ đường trung tuyến AM, đường trung trực của cạnh AC cắt AB tại D. Trên cạnh AC lấy điểm E sao cho CE = BD. Khẳng định nào sau đây sai?

• A. BE vuông góc với AC;
• B. CD vuông góc với AB;
• C. Ba đường thẳng AM, BE, CD đồng quy tại một điểm;

• D. Ba đường thẳng AM, BE, CD không đồng quy tại một điểm.

Câu 5: Trong một tam giác, trực tâm là giao điểm của ba đường nào?

• A. Đường phân giác;
• B. Đường trung tuyến;
• C. Đường trung trực;

• D. Đường cao.

Câu 6: Cho ∆ABC nhọn có H là trực tâm. Trực tâm của ∆HAB là:

• A. Điểm B;
• B. Điểm H;

• C. Điểm C;

• D. Điểm A.

Câu 7: Cho ∆ABC có $\widehat{A}$ =70°, AB < AC. Tia phân giác $\widehat{A}$ cắt BC tại D, kẻ BF ⊥ AC tại F, lấy điểm E thuộc AC sao cho AE = AB. Gọi H là giao điểm của AD và BF.

Cho các khẳng định sau:

(I) H là trực tâm của ∆ABE;

(II)$\widehat{FHD}$ =160°.

Chọn câu trả lời đúng nhất.

• A. Chỉ (I) đúng;

• B. Chỉ (II) đúng;
• C. Cả (I), (II) đều đúng;
• D. Cả (I), (II) đều sai.

Câu 8: Cho ∆ABC cân tại A có M là trung điểm BC, đường cao CN cắt AM tại H. Một tính chất của cặp đường thẳng BH và AC là:

• A. BH // AC;
• B. BH trùng AC;
• C. BH cắt AC nhưng không vuông góc với AC;

• D. BH ⊥ AC.

Câu 9: Cho ∆ABC có $\widehat{A}$ > 90°, AD vuông góc với BC tại D, BE vuông góc với AC tại E. Gọi F là giao điểm của đường thẳng AD và BE. Khẳng định nào sau đây đúng?

• A. AB ⊥ FC;

• B. AB // FC;
• C. AB cắt FC nhưng không vuông góc với FC;
• D. AB trùng FC.

Câu 10: Cho ∆ABC vuông tại A, đường trung tuyến BM. Qua M vẽ một đường thẳng vuông góc với BC, cắt đường thẳng AB tại D. Vẽ điểm E sao cho M là trung điểm DE. Cho các khẳng định sau:

(I) M là trực tâm của DBCD.

(II) AE // DC.

(III) AE ⊥ BM;

Số khẳng định đúng là:

• A. 0;
• B. 1;
• C. 2;

• D. 3.

Câu 11: Cho ∆ABC cân tại A có $\widehat{A}$ =70°, đường cao BH cắt đường trung tuyến AM (M ∈ BC) tại K. Khẳng định nào sau đây đúng nhất?

• A. K là trực tâm của ∆ABC;
• B. CK ⊥ AB;
• C. $\widehat{HKM}$ =110°;

• D. Cả A, B đều đúng.

Câu 12: Cho ∆ABC vuông tại A, đường cao AH. Gọi M, N lần lượt là trung điểm của AH và CH. Một tính chất của cặp đường thẳng BM và AN là:

• A. BM trùng AN;
• B. BM cắt AN nhưng không vuông góc với AN;

• C. BM ⊥ AN;

• D. BM // AN.

Câu 13: Cho ∆ABC cân tại A. Gọi H là trực tâm của ∆ABC và $\widehat{BAH}$ =30°. Xét hai khẳng định sau:

(I) ∆ABC là tam giác vuông cân;

(II) ∆ABC là tam giác đều.

Chọn câu trả lời đúng.

• A. Chỉ (I) đúng;

• B. Chỉ (II) đúng;

• C. Cả (I) và (II) đều đúng;
• D. Cả (I) và (II) đều sai.

Câu 14: Cho ∆ABC có BD và CE lần lượt là các đường cao hạ từ B, C và BD = CE. Gọi H là giao điểm của BD và CE. Khẳng định nào sau đây sai?

• A. ∆ABC cân tại A;

• B. ∆ABC cân tại B;

• C. H là trực tâm của ∆ABC;
• D. AH là đường phân giác của ∆ABC.

Câu 15: Chọn phát biểu sai trong các câu sau.

• A. Ba đường trung tuyến của tam giác đồng quy;
• B. Ba đường phân giác của tam giác đồng quy;
• C. Ba đường trung trực của tam giác đồng quy;

• D. Ba đường cao của tam giác không đồng quy.

Câu 16: Cho hình vẽ dưới đây. Đường cao của tam giác ABC là

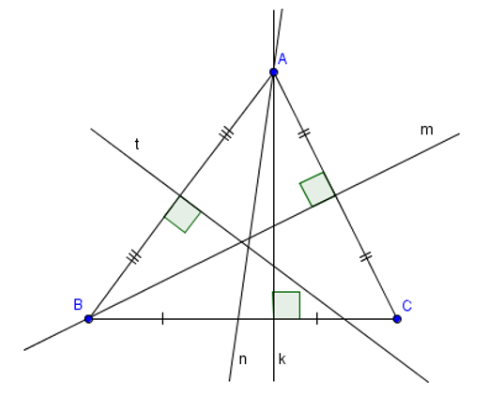
• A. m; t và k;
• B. m và n;

• C. m và k;

• D. m và t.

Câu 17: Cho ∆ABC đều có G là trọng tâm của tam giác. Trực tâm của ∆GAB là:

• A. Điểm G;
• B. Điểm B;
• C. Điểm A;

• D. Điểm C.

Câu 18: Cho ∆ABC vuông tại A. Trên cạnh AC lấy điểm M bất kì (M ≠ A, C). Qua M kẻ đường thẳng vuông góc với BC tại N. Từ C kẻ đường thẳng vuông góc với BM tại P. Gọi D là giao điểm của AB và CP. Khẳng định nào sau đây sai?

• A. M là trực tâm của ∆DBC;
• B. DM ⊥ BC;
• C. M, N, D thẳng hàng;

• D. AB, MN, CP không đồng quy tại điểm D.

Câu 19: Cho ∆ABC vuông tại A. Trực tâm của tam giác ABC là

• A. điểm M trung điểm của BC;
• B. điểm H nằm trong tam giác ABC;

• C. điểm A;

• D. điểm O cách đều ba cạnh của tam giác ABC.

Câu 20: Cho ∆ABC nhọn có AH ⊥ BC (H ∈ BC). Trên AH lấy điểm D sao cho $\widehat{HAB}=\widehat{HCD}$. Một tính chất của cặp đường thẳng BD và AC là:

• A. BD trùng AC;
• B. BD // AC;

• C. BD ⊥ AC;

• D. BD cắt AC nhưng không vuông góc với AC.