I. ĐƯỜNG CAO CỦA TAM GIÁC

HĐ1:

Kết luận: Trong một tam giác, đoạn vuông góc kẻ từ một đỉnh đến đường thẳng chứa cạnh đối diện gọi là một đường cao của tam giác đó.

Ví dụ:

AM là đường cao của tam giác ABC.

Ví dụ 1 (SGK -tr116)

• Đoạn thẳng AH, DN không là đường cao của tam giác ABC.
• Đoạn thẳng BK là đường cao của tam giác ABC.

Ví dụ 2 (SGK -tr116)

LT1:

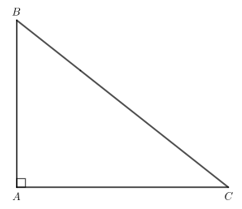
Đường cao đi qua B và vuông góc với AC là AB.

Đường cao đi qua C và vuông góc với AB là AC.

Nhận xét:

• Mỗi tam giác có ba đường cao.
• Đường cao của tam giác có thể nằm trong, trên cạnh, hoặc nằm ngoài tam giác.

II. TÍNH CHẤT BA ĐƯỜNG CAO CỦA TAM GIÁC

HĐ2:

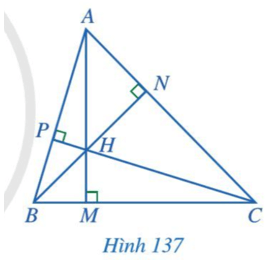
Ba đường cao AM, BN, CP của tam giác ABC cùng đi qua điểm H.

Định lí: Trong một tam giác, ba đường cao cùng đi qua một điểm. Điểm đó được gọi là trực tâm của tam giác.

Nhận xét: Để xác định giao điểm ba đường trung trực của một tam giác, ta chỉ cần vẽ hai đường trung trực bất kì và xác định giao điểm của hai đường đó.

Ví dụ 3 (SGK -tr117)

LT2:

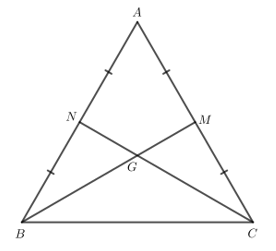
Gọi M, N theo thứ tự là trung điểm của AC và AB.

Do tam giác ABC đều nên AB = BC = CA và $\widehat{BAC}=\widehat{ABC}=\widehat{ACB}$.

Do M là trung điểm của AC nên AM = CM.

Xét ∆BAM và ∆BCM có:

BA = BC (chứng minh trên).

$\widehat{BAM}=\widehat{BCM}$

AM = CM (chứng minh trên).

Do đó ∆BAM = ∆BCM (c - g - c).

Suy ra $\widehat{BMA}=\widehat{BMC}$ (2 góc tương ứng).

Mà $\widehat{BMA}+\widehat{BMC}$ = 180° nên $\widehat{BMA}=\widehat{BMC}$ = 90°

Do đó BM là đường cao của tam giác ABC.

Tương tự CN là đường cao của tam giác ABC.

Tam giác ABC có hai đường cao BM và CN cắt nhau tại G nên G là trực tâm của tam giác ABC.

Ví dụ 4 (SGK -tr118)

LT3:

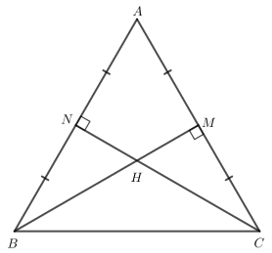
Gọi M, N lần lượt là trung điểm của AC và AB.

Do H là trực tâm của tam giác ABC nên CH ⊥ AB, BH ⊥ AC hay CN ⊥ AB, BM ⊥ AC.

Lại có H là trọng tâm của tam giác ABC nên BM, CN là các đường trung tuyến của tam giác ABC.

Khi đó BM vuông góc với AC tại trung điểm M của AC nên BM là đường trung trực của đoạn thẳng AC.

Do đó BA = BC (1).

Do CN vuông góc với AB tại trung điểm N của AB nên CN là đường trung trực của đoạn thẳng AB.

Do đó CA = CB (2).

Từ (1) và (2) suy ra AB = BC = CA nên tam giác ABC đều.