Câu 1: Cho ba số tự nhiên liên tiếp biết tích của hai số trước kém tích của hai số sau là 28. Ba số tự nhiên đó là

• A. 12; 13; 14;

• B. 13; 14; 15;

• C. 14; 15; 16;
• D. 15; 16; 17.

Câu 2: Bậc của đa thức $5x^{2}(2x^{3} – 4x^{2} + 3x – 1)$ là

• A. 10;

• B. 5;

• C. 6;
• D. Không xác định.

Câu 3: Cho hai đa thức: $P(x) = 2x^{3} – 2x – (5x + 10) – 2x^{2} + 4x$ và $Q(x) = 2x^{3} – 3x^{2} – 2 – (3x – 2) – x^{2}$. Tìm H($\frac{1}{2})$ biết H(x) = P(x) – Q(x).

• A. 0
• B. $\frac{1}{2}$

• C. $-\frac{19}{2}$

• D. 10

Câu 4: Cho đa thức $G(x) = – x^{5} + 2x^{3} – 4x^{2} + 20$ và đa thức $H(x) =\frac{1}{2}x^{5}-x^{3}+\frac{5}{2}x^{2}-18$  Đa thức P(x) = G(x) + 2H(x) có nghiệm là

• A. x = 4; x = – 4;

• B. x = 4;
• C. x = 16;
• D. x = 2.

Câu 5: Phép chia $(x^{5} – 3x^{4} + 4x^{3} + 2x^{2} + 3x + 10) : (x^{2} + 1)$ có kết quả là

• A. $x^{3} – 3x^{2} + 3x + 5$ dư 5;

• B. $x^{3} – 3x^{2} + 3x + 5$;
• C. $x^{3} – 3x^{2} + 3x + 10$;
• D. $x^{3} – 3x^{2} + 3x + 15$ dư 5.

Câu 6: Một xe khách đi từ Hà Nội đến Quảng Ninh với vận tốc 60 km/h. Sau đó 45 phút, một xe du lịch cũng đi từ Hà Nội đến Quảng Ninh với vận tốc 75 km/h. Cả hai xe đều không nghỉ dọc đường.Gọi A(x) là đa thức biểu thị quãng đường xe du lịch đi được và B(x) là đa thức biểu thị quãng đường xe khách đi được kể từ khi xuất phát đến khi xe du lịch đi được x giờ.

Tính G(3). Biết G(x) = A(x) – B(x).

• A. G(3) = 1;

• B. G(3) = 0;

• C. G(3) = 2;
• D. G(3) = – 1.

Câu 7: Cho hình chữ nhật có chiều dài là a, chiều rộng là b. Biểu thức biểu thị chu vi hình chữ nhật đó là

• A. a + b;
• B. 2a + b;
• C. a + 2b;

• D. 2(a + b).

Câu 8: Giá trị của biểu thức T = x + 2 tại x = − 2 là

• A. − 2;
• B. 2;
• C. 4;

• D. 0.

Câu 9: Giá trị của biểu thức: xy(x + y) + (x – y)$^{2}$ tại x = – 4 và y = 2.

• A. 52;

• B. 20;
• C. – 20;
• D. – 52.

Câu 10: Tìm số nguyên x để phép chia $10x^{4} – 13x^{3} – 9x^{2} + x + 18$ chia hết cho 2x – 3.

• A. x ∈ {0; 1; 2; 3};

• B. x ∈ {± 1; ± 2; ± 3; ± 6};
• C. x ∈ {2; 3};
• D. x ∈ {1; 2; 3; 6}.

Câu 11: Hệ số cao nhất của đa thức $Q(x) = – 10x^{4} + x^{4} + 19x^{3} + x + 10x + 7$ là

• A. – 10;
• B. 19;

• C. – 9;

• D. 7.

Câu 12: Với mọi số nguyên n, đa thức $n^{2}(3 – 2n) – n(3n – 2n^{2} – 3)$ luôn chia hết cho số nào dưới đây?

• A. 2

• B. 3

• C. 4
• D. 5

Câu 13: Cho đa thức G(x) thỏa mãn: xG(x + 1) = (x – 2)G(x)

Một trong các nghiệm của đa thức G(x) là

• A. x = 0;

• B. x = – 1;
• C. x = – 2;
• D. Không xác định.

Câu 14: Cho đa thức $F(x) = x^{4} – 9x^{3} + 21x^{2} + ax + b$ và $G(x) = x^{2} – x – 2$.

Để đa thức F(x) chia hết cho đa thức G(x) thì a và b là

• A. a = 1 và b = – 30;

• B. a = – 1 và b = 30;
• C. a = 0 và b = 0;
• D. Không xác định.

Câu 15: Từ một tấm tôn hình vuông có kích thước 50 cm, Minh cắt đi ở mỗi góc của tấm bìa một hình vuông sao cho bốn hình vuông bị cắt đi có cùng độ dài cạnh là x, sau đó gấp lại để tạo thành hình hộp chữ nhật không nắp (hình vẽ). Đa thức biểu diễn thể tích của hình hộp chữ nhật được tạo thành theo độ dài cạnh của hình vuông bị cắt đi là

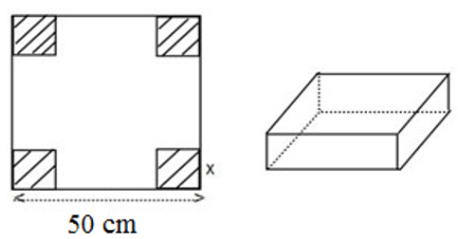
• A. $4x^{3} – 200x^{2} + 250x;$
• B. $4x^{3} + 200x^{2} + 2500x;$
• C. $4x^{3} + 200x^{2} + 250x;$

• D. $4x^{3} – 200x^{2} + 2500x$.

Câu 16: Bậc của đa thức một biến $5x^{3} + 6x^{2} – 6x – 5x^{3} + 4x + 1$ là

• A. 5;
• B. 3;
• C. 6;

• D. 2.

Câu 17: Cho hai biểu thức A = 5x – 3y và B = 5x + 3y. Khẳng định nào dưới đây đúng?

• A. A = B tại x = 3 và y = – 5;
• B. A < B tại x = 3 và y = – 5;

• C. A > B tại x = 3 và y = – 5;

• D. A ≤ B tại x = 3 và y = – 5.

Câu 18: Trong tháng 8 nhà ông Nam dùng hết 137 số điện. Hỏi ông Nam phải trả bao nhiêu tiền điện, biết đơn giá điện như sau:

Giá tiền cho 50 số đầu tiên là x đồng/số;

Giá tiền cho 50 số tiếp theo (từ số 51 đến số 100) là y đồng/số;

Giá tiền cho 100 số tiếp theo (từ 101 đến số 200) là z đồng/số.

Biểu thức tính số tiền điện nhà ông Nam và số tiền điện nhà ông Nam phải trả khi x = 1 678; y = 1 734 và z = 2 014 là

• A. 50x + 50y + 37z và 245 118 đồng;

• B. 137(x + y + z) và 734 362 đồng;
• C. 50x + 50y + 37z và 254 118 đồng;
• D. 137(x + y + z) và 743 362 đồng.

Câu 19: Một vận động viên leo núi nhận thấy rằng càng lên cao nhiệt độ không khí càng giảm. Mối liên hệ giữa nhiệt độ không khí T (℃) và độ cao x (m) so với chân núi được cho bởi công thức $T =-\frac{3}{500}x +23$ Bạn Thắng đang leo núi và dùng nhiệt kế đo được nhiệt độ không khí tại vị trí dừng chân là 15,8℃. Hỏi bạn Thắng đang ở độ cao bao nhiêu mét so với chân núi?

• A. 1 200 mét;

• B. 1 000 mét;
• C. 900 mét;
• D. Không xác định.

Câu 20: Nhân dịp khai trương, một cửa hàng sau khi giảm giá 20 nghìn đồng mỗi sản phẩm so với giá ban đầu là 3x (nghìn đồng) thì có doanh thu là 6x$^{2}$ + 170x – 1 400 (nghìn đồng). Số sản phẩm mà cửa hàng đã bán được theo x là

• A. 2x + 700 (sản phẩm);
• B. 20x + 70 (sản phẩm);
• C. 20x + 700 (sản phẩm);

• D. 2x + 70 (sản phẩm).